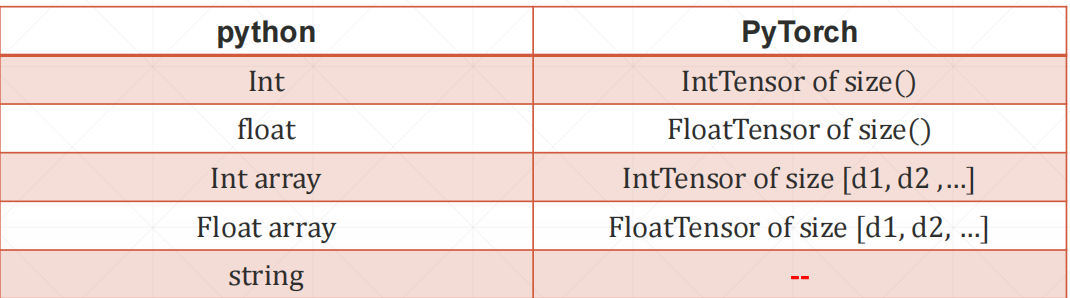
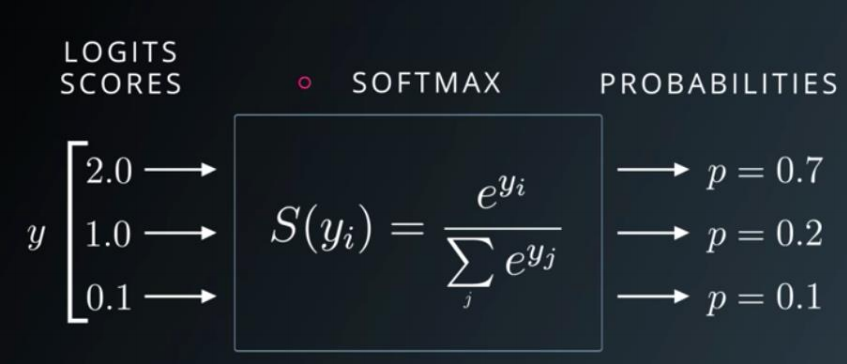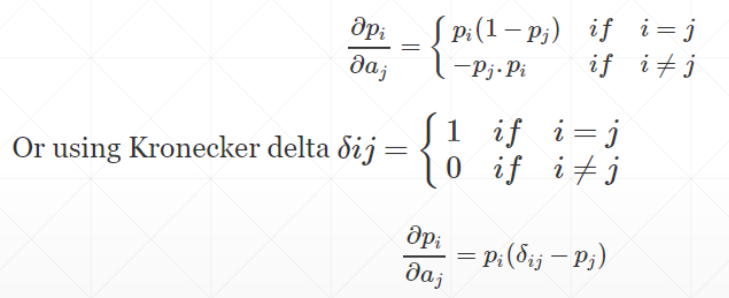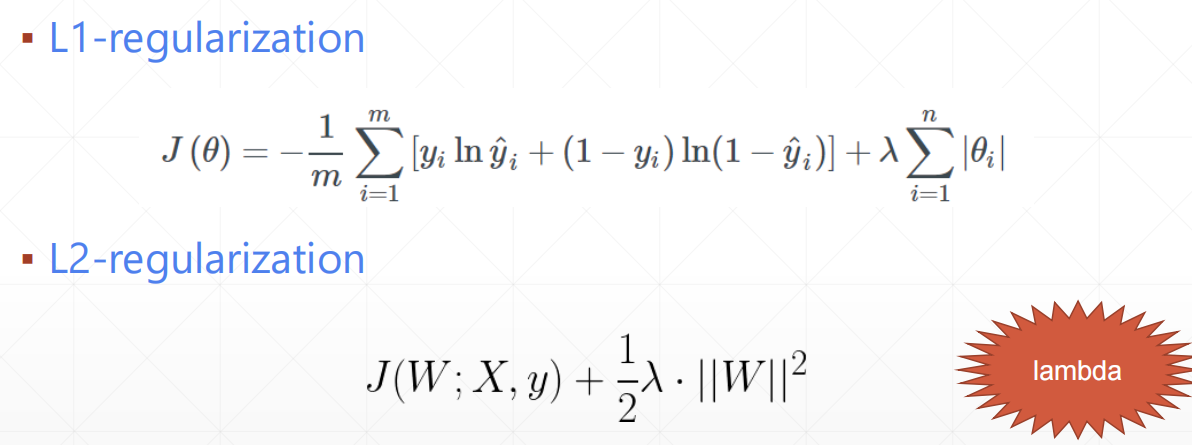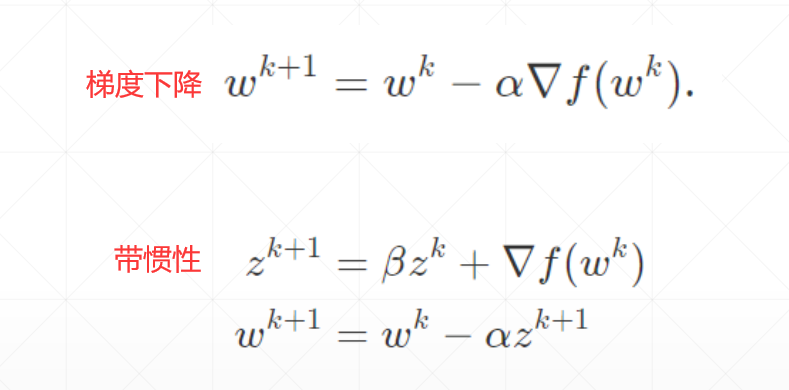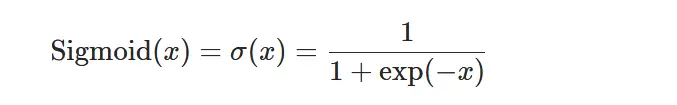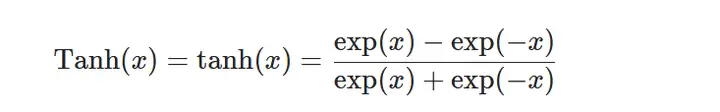基本数据类型
类型检验 1 2 3 4 5 6 7 8 9 10 11 12 data = torch.randn(2 , 3 ) print (data.type ())print (type (data)) print (isinstance (data, torch.FloatTensor))print (isinstance (data, torch.cuda.FloatTensor))data = data.cuda() print (isinstance (data, torch.cuda.FloatTensor))
张量和维度 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 data = torch.tensor(1. ) print ("data.shape:" , data.shape)print ("data.size():" , data.size())print ("data.ndimension():" , data.ndimension())print ('----------------------------------------------' )data = torch.tensor([1.1 ]) data = torch.tensor([1.1 , 2.2 ]) data = torch.FloatTensor(1 ) data = torch.FloatTensor(2 ) print (data)data = torch.from_numpy(np.ones(2 )) print ("data.shape:" , data.shape)print ("data.size():" , data.size())print ("data.ndimension():" , data.ndimension())print ('----------------------------------------------' )data = torch.randn(2 , 3 ) print ("data.shape:" , data.shape)print ("data.shape[0]:" , data.shape[0 ])print ("data.size(0):" , data.size(0 ))print ("data.size(1):" , data.size(1 ))print ("data.ndimension():" , data.ndimension())print ('----------------------------------------------' )data = torch.randn(2 , 2 , 3 ) print ("data.shape:" , data.shape)print ("data.size():" , data.size())print ("data.ndimension():" , data.ndimension())data = torch.randn(2 , 3 , 28 , 28 ) print (data)print ("data.shape:" , data.shape)print ("data.size():" , data.size())print ("data.ndimension():" , data.ndimension())print (data.numel()) print (data.dim())
创建Tensor 通过list创建 1 2 3 4 data = torch.tensor([2. , 3.2 ]) data = torch.FloatTensor([2. , 3.2 ]) data = torch.tensor([[2. , 3.2 ], [1. , 0.5 ]])
通过numpy创建 1 2 3 4 5 a = np.array([2 , 3.3 ]) data = torch.from_numpy(a) a = np.ones([2 , 3 ]) data = torch.from_numpy(a)
empty() 1 2 3 4 5 6 7 8 9 data = torch.empty(2 , 3 ) print (data)data = torch.FloatTensor(1 , 2 , 3 ) print (data)data = torch.IntTensor(1 , 2 , 3 ) print (data)
set_default_tensor_type() 1 2 3 4 print (torch.tensor([1.2 , 3 ]).type ()) torch.set_default_tensor_type( torch.DoubleTensor) print (torch.tensor([1.2 , 3 ]).type ())
rand/randn()
full() 1 2 3 data = torch.full([2 , 3 ], 6 ) print (data)
arange() 1 2 3 4 data = torch.arange(0 , 10 , 2 ) data = torch.linspace(0 , 10 , steps=11 ) data = torch.logspace(0 , -1 , steps=11 )
zeros/ones/eye() 1 2 3 4 data = torch.zeros(3 , 3 ) data = torch.ones(3 , 3 ) data = torch.eye(3 )
randperm() 1 2 3 4 5 6 7 8 9 10 data = torch.randperm(10 ) print (data)a = torch.rand(4 , 3 ) b = torch.rand(4 , 2 ) print (a, '\n' , b)idx = torch.randperm(4 ) print (idx)print (a[idx], '\n' , b[idx])
索引与切片 四个维度 batch,channel,height,width
1 2 3 4 5 6 a = torch.rand(4 , 3 , 28 , 28 ) print (a[0 ].shape)print (a[0 , 0 ].shape)print (a[0 , 0 , 0 ].shape)print (a[0 , 0 , 0 , 0 ].shape)print (a[0 , 1 , 2 , 4 ])
基本切片 1 2 3 4 5 print (a[:2 ].shape)print (a[:2 , :1 , :, :].shape)print (a[:2 , -3 :, :, :].shape)print (a[[0 , 1 , 3 ], -3 :, :, :].shape)
隔点采样 1 2 3 print (a[:, :, 0 :28 :2 , 0 :28 :2 ].shape) print (a[:, :, ::2 , ::2 ].shape)
a.index_select() 1 2 3 4 print (a.index_select(0 , torch.tensor([0 , 1 , 2 ])).shape) print (a.index_select(1 , torch.tensor([0 , 1 ])).shape) print (a.index_select(2 , torch.arange(0 , 28 , 2 )).shape)
… 1 2 3 print (a[0 , ...]) print (a[..., :2 ])
masked_select() 1 2 3 4 x = torch.randn(3 , 4 ) mask = x.ge(0.5 ) print (torch.masked_select(x, mask))
take() 1 2 3 x = torch.tensor([[4 , 3 , 5 ], [6 , 7 , 8 ]]) print (torch.take(x, torch.tensor([0 , 2 , 5 ])))
维度变换 view/reshape 1 2 3 4 5 6 7 8 a = torch.rand(4 , 1 , 28 , 28 ) print (a.shape)a = a.view(4 , 28 * 28 ) print (a.shape)a = a.reshape(4 * 28 , 28 ) print (a.shape)
unsqueeze/squeeze 拉伸/挤压 1 2 3 4 a = torch.rand(4 , 1 , 28 , 28 ) print (a.unsqueeze(0 ).shape) print (a.unsqueeze(-1 ).shape)
1 2 3 4 5 6 7 b = torch.rand(32 ) b = b.unsqueeze(1 ).unsqueeze(2 ).unsqueeze(0 ) print (b.shape)print (b.squeeze().shape) print (b.squeeze(0 ).shape)print (b.squeeze(1 ).shape)
expand/repeat 扩张/重复 1 2 3 4 5 6 7 8 f = torch.rand(4 , 32 , 14 , 14 ) b = torch.rand(32 ) b = b.unsqueeze(1 ).unsqueeze(2 ).unsqueeze(0 ) b = b.expand(4 , 32 , 14 , 14 ) b = b.expand(-1 , 32 , -1 , -1 ) print (b.shape)
1 2 3 4 5 b = torch.rand(32 ) b = b.unsqueeze(1 ).unsqueeze(2 ).unsqueeze(0 ) b = b.repeat(4 , 1 , 14 , 14 ) print (b.shape)
转置 t 1 2 3 4 a = torch.tensor([[1 , 2 ], [3 , 4 ]]) print (a.t())
transpose 维度交换 1 2 3 4 5 6 7 8 a = torch.rand(4 , 3 , 14 , 14 ) a1 = a.transpose(1 , 3 ).contiguous().view(4 , 3 * 14 * 14 ).view(4 , 3 , 14 , 14 ) a2 = a.transpose(1 , 3 ).contiguous().view(4 , 3 * 14 * 14 ).view(4 , 14 , 14 , 3 ).transpose(1 , 3 ) print (torch.all (torch.eq(a, a1)))print (torch.all (torch.eq(a, a2)))
permute 维度排列 1 2 3 4 a = torch.rand(4 , 3 , 14 , 7 ) a1 = a.permute(0 , 2 , 3 , 1 ) print (a1.shape)
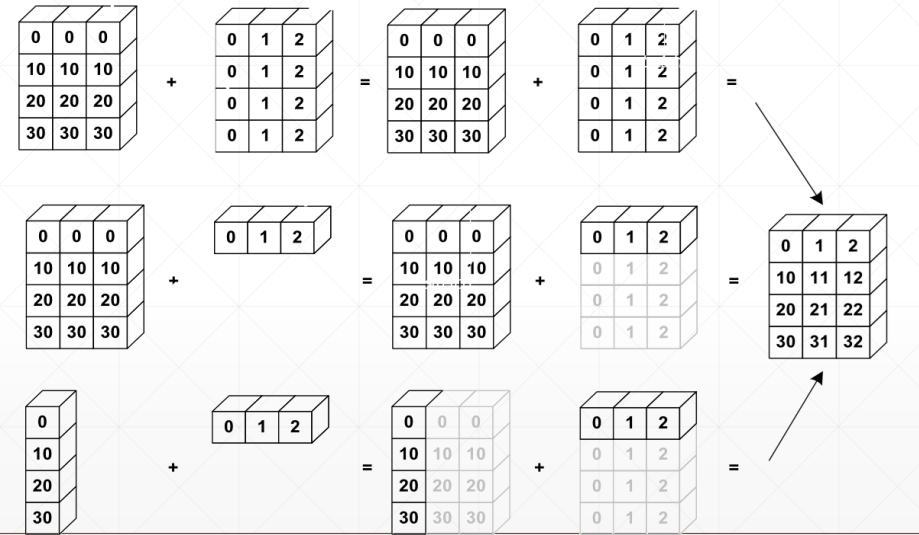
Broadcast机制
broadcast广播/自动扩张机制
主要思想
在前面插入维度,使维度一致
扩张size为1的维度使得size一致
为什么需要broadcast
可以broadcast的情况
从最后一维往前开始匹配
如果当前维度为1,扩展size到一致
如果往前没有维度,则插入一个维度,并扩展size到一致
其他情况都是不能broadcast的
拼接与拆分 cat 要求除dim=d外,其他维度size一致
1 2 3 4 5 6 7 8 9 10 11 12 13 14 a1 = torch.rand(4 , 3 , 16 , 16 ) a2 = torch.rand(5 , 3 , 16 , 16 ) b = torch.cat([a1, a2], dim=0 ) print (b.size())a1 = torch.rand(4 , 2 , 16 , 16 ) a2 = torch.rand(4 , 1 , 16 , 16 ) b = torch.cat([a1, a2], dim=1 ) print (b.size())a1 = torch.rand(4 , 3 , 16 , 16 ) a2 = torch.rand(4 , 3 , 16 , 16 ) b = torch.cat([a1, a2], dim=2 ) print (b.size())
stack 要求所有维度一致,会在dim=d维度前新增一个维度
1 2 3 4 a1 = torch.rand(4 , 3 , 16 , 16 ) a2 = torch.rand(4 , 3 , 16 , 16 ) b = torch.stack([a1, a2], dim=2 ) print (b.size())
split 按照长度拆分
1 2 3 4 5 6 a = torch.rand(3 , 3 , 16 , 16 ) aa, bb = a.split([2 , 1 ], dim=0 ) print (aa.size(), bb.size())aa, bb, cc = a.split(1 , dim=0 ) print (aa.size(), bb.size(), cc.size())
chunk 按照数量拆分
1 2 3 4 5 a = torch.rand(3 , 3 , 16 , 16 ) aa, bb = a.chunk(2 , dim=0 ) aa, bb, cc = a.chunk(3 , dim=0 ) print (aa.size(), bb.size(), cc.size())
基本运算 加减乘除 +=*/ 或者add,sub,mul,div
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 a = torch.rand(3 , 4 ) b = torch.rand(4 ) c1 = a + b c2 = a.add(b) print (torch.all (torch.eq(c1, c2)))c1 = a - b c2 = a.sub(b) print (torch.all (torch.eq(c1, c2)))c1 = a * b c2 = a.mul(b) print (torch.all (torch.eq(c1, c2)))c1 = a / b c2 = a.div(b) print (torch.all (torch.eq(c1, c2)))
matmul矩阵相乘
mm 只支持二维
matmul
@
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 a = torch.tensor([[1. , 2. ], [3. , 4. ]]) b = torch.ones(2 , 2 ) c = torch.mm(a, b) print (c)c = torch.matmul(a, b) print (c)c = a @ b print (c)x = torch.rand(4 , 784 ) w = torch.rand(512 , 784 ) print ((x @ w.t()).shape)a = torch.rand(4 , 3 , 28 , 64 ) b = torch.rand(4 , 3 , 64 , 32 ) c = torch.rand(4 , 1 , 64 , 32 ) print (torch.matmul(a, b).size())print (torch.matmul(a, c).size())
pow/次方 1 2 3 4 5 6 7 8 9 a = torch.full([2 , 2 ], 3 ) print (a.pow (2 ))print (a ** 2 )print (a.pow (0.5 ))print (a ** 0.5 )print (a.sqrt())print (a.rsqrt())
exp/log 1 2 print (torch.exp(torch.ones(2 , 2 )))print (torch.log(torch.ones(2 , 2 )))
近似(取整) 1 2 3 4 5 6 a = torch.tensor(3.14 ) print (a.floor()) print (a.ceil()) print (a.round ()) print (a.trunc()) print (a.frac())
clamp限幅 1 2 3 4 grad = torch.rand(2 , 3 ) * 15 print (a.max (), a.median(), a.min ())print (grad.clamp(10 )) print (grad.clamp(0 , 10 ))
比较运算 1 2 3 4 5 6 7 8 9 a = torch.randn(2 , 3 ) b = torch.randn(2 , 3 ) print (a, '\n' , b)print (a > b, '\n' , a.gt(b))print (a >= b, '\n' , a.ge(b))print (a != b)print (a == b)print (torch.eq(a, b), torch.equal(a, b))
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 tensor([[-1.9149 , 0.2055 , -0.9794 ], [ 0.0520 , 1.4960 , -0.3995 ]]) tensor([[-0.2851 , -0.4754 , -0.9211 ], [ 2.2437 , -2.5068 , 0.0198 ]]) tensor([[False , True , False ], [False , True , False ]]) tensor([[False , True , False ], [False , True , False ]]) tensor([[False , True , False ], [False , True , False ]]) tensor([[False , True , False ], [False , True , False ]]) tensor([[True , True , True ], [True , True , True ]]) tensor([[False , False , False ], [False , False , False ]]) tensor([[False , False , False ], [False , False , False ]]) False
统计属性 norm范数 1 2 3 4 5 6 7 8 9 10 11 12 print (a.norm(1 ), '\n' , b.norm(1 ), '\n' , c.norm(1 ))print (a.norm(2 ), '\n' , b.norm(1 ), '\n' , c.norm(2 ))print (b.norm(1 , dim=0 ))print (b.norm(1 , dim=1 ))c = torch.tensor([[[1. , 1. ], [1. , 1. ]], [[2. , 2. ], [2. , 2. ]]]) print (c.norm(1 , dim=0 ))print (c.norm(1 , dim=1 ))
min/max/mean/prod 1 2 3 4 5 6 7 a = torch.arange(1 , 11 ).view(2 , 5 ).float () print (a)print (a.min ())print (a.max ())print (a.mean())print (a.prod())
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 a = torch.rand(3 , 4 ) print (a)print (a.min (dim=0 , keepdim=True ))print (a.min (dim=0 ))print (a.max (dim=0 ))print (a.mean(dim=0 ))print (a.prod(dim=0 ))""" tensor([[0.9035, 0.6971, 0.4886, 0.7893], [0.1721, 0.7944, 0.0457, 0.7884], [0.9295, 0.3432, 0.1493, 0.7428]]) torch.return_types.min(values=tensor([[0.1721, 0.3432, 0.0457, 0.7428]]),indices=tensor([[1, 2, 1, 2]])) torch.return_types.min(values=tensor([0.1721, 0.3432, 0.0457, 0.7428]),indices=tensor([1, 2, 1, 2])) torch.return_types.max(values=tensor([0.9295, 0.7944, 0.4886, 0.7893]),indices=tensor([2, 1, 0, 0])) tensor([0.6684, 0.6116, 0.2279, 0.7735]) tensor([0.1445, 0.1901, 0.0033, 0.4623]) """ print (a.min (dim=1 , keepdim=True )) print (a.min (dim=1 ))print (a.max (dim=1 ))print (a.mean(dim=1 ))print (a.prod(dim=1 ))""" tensor([[0.7369, 0.7026, 0.7261, 0.6016], [0.1645, 0.3403, 0.6544, 0.4276], [0.5673, 0.4806, 0.7130, 0.7522]]) torch.return_types.min( values=tensor([[0.6016], [0.1645], [0.4806]]), indices=tensor([[3], [0], [1]])) torch.return_types.min(values=tensor([0.6016, 0.1645, 0.4806]),indices=tensor([3, 0, 1])) torch.return_types.max(values=tensor([0.7369, 0.6544, 0.7522]),indices=tensor([0, 2, 3])) tensor([0.6918, 0.3967, 0.6283]) tensor([0.2262, 0.0157, 0.1462]) """
argmax/argmin 1 2 3 print (a.argmax())print (a.argmin())
topk/kthvalue 1 2 3 4 5 6 # 取前k大/小的值 topK # 取第k小的值 kthvalue a = torch.arange(1, 11).view(2, 5).float() print(a.topk(3, dim=1)) print(a.topk(3, dim=1, largest=False)) # largest=False取前k小 print(a.kthvalue(2, dim=1)) # 取前k小
高级操作 where 根据条件tensor赋值
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 condition = torch.rand(2 , 2 ) print (condition, '\n' , condition > 0.5 )a = torch.zeros_like(condition) b = torch.ones_like(condition) c = torch.where(condition > 0.5 , a, b) print (c)""" tensor([[0.8901, 0.9493], [0.7294, 0.4096]]) tensor([[ True, True], [ True, False]]) tensor([[0., 0.], [0., 1.]]) """
gather 根据索引tensor找值
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 prob = torch.randn(4 , 10 ) idx = prob.topk(3 , dim=1 ) print (idx[0 ])label = torch.arange(10 ) + 100 print (label)res = torch.gather(label.expand(4 , 10 ), dim=1 , index=idx[0 ].long()) print (res)""" torch.return_types.topk( values=tensor([[1.2671, 1.1393, 0.4483], [1.3529, 0.8119, 0.7457], [0.7395, 0.7150, 0.6264], [0.9675, 0.7654, 0.6994]]), indices=tensor([[2, 6, 7], [5, 0, 1], [7, 4, 0], [0, 6, 2]])) tensor([100, 101, 102, 103, 104, 105, 106, 107, 108, 109]) tensor([[102, 106, 107], [105, 100, 101], [107, 104, 100], [100, 106, 102]]) """
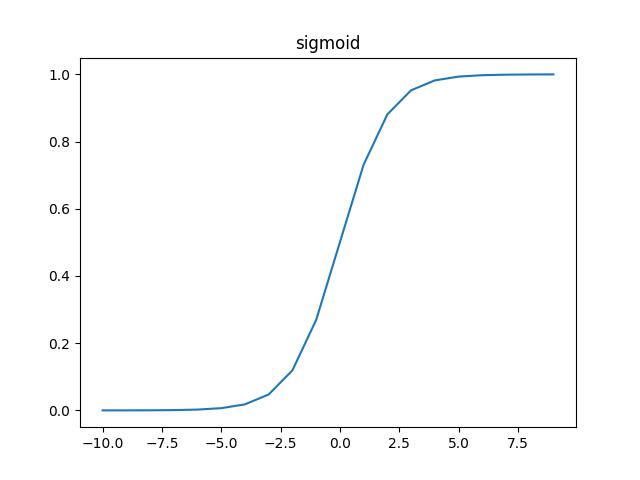
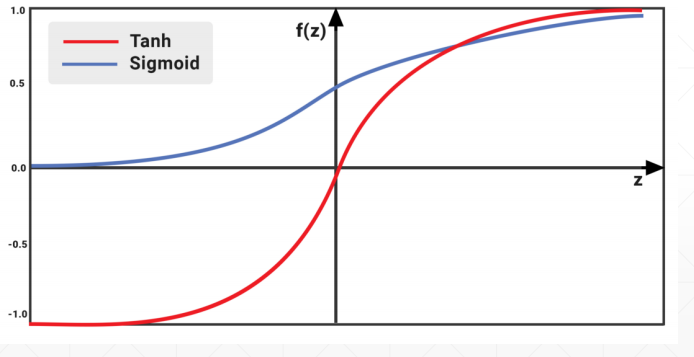
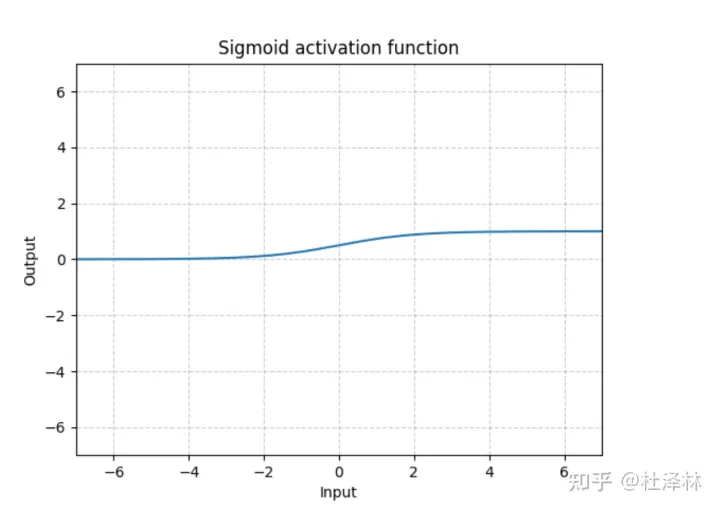
常见激活函数 sigmoid 1 2 3 4 5 a = torch.arange(-10 , 10 , 1 ) b = torch.sigmoid(a) plt.plot(a, b) plt.title("sigmoid" ) plt.show()
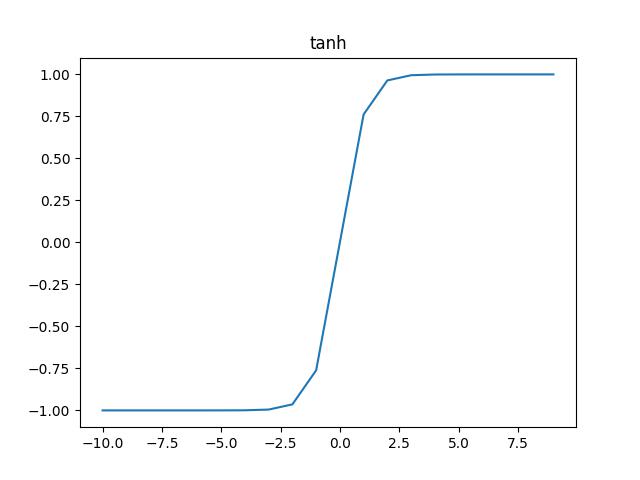
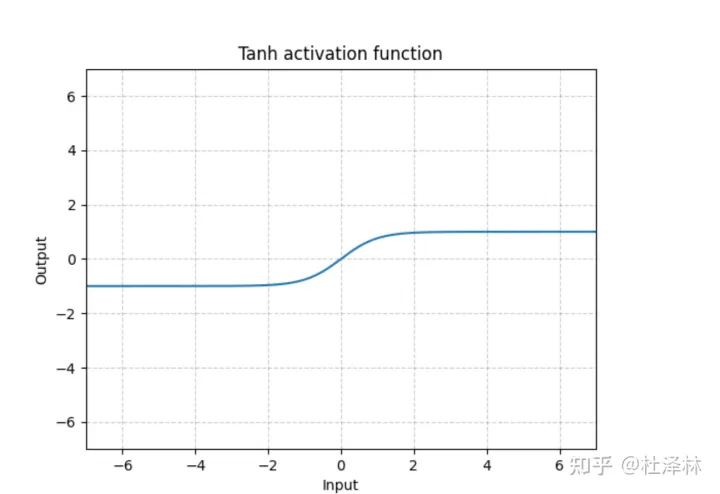
tanh 1 2 3 4 b = torch.tanh(a) plt.plot(a, b) plt.title("tanh") plt.show()
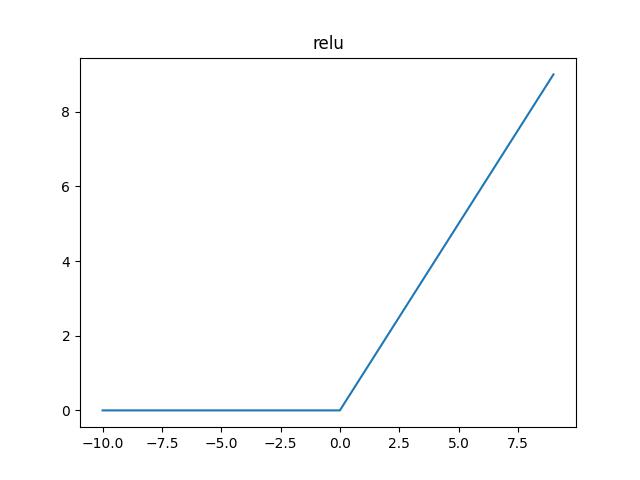
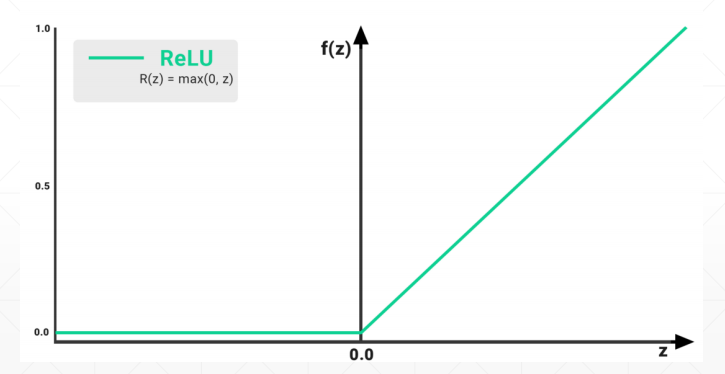
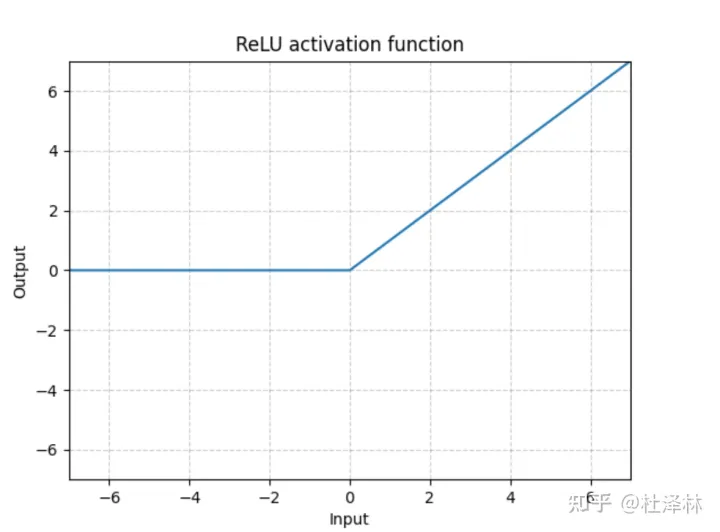
relu 1 2 3 4 5 b = torch.relu(a) plt.plot(a, b) plt.title("relu") plt.savefig("relu.jpg") plt.show()
损失和梯度 torch.autograd.grad 1 2 3 4 5 6 7 8 9 10 11 12 13 14 import torchimport torch.nn.functional as Fx = torch.ones(1 ) w = torch.tensor([2. ]) w.requires_grad_() mse = F.mse_loss(torch.ones(1 ), x * w) print (torch.autograd.grad(mse, [w])) x = torch.ones(1 ) w = torch.tensor([2. ], requires_grad=True ) mse = F.mse_loss(torch.ones(1 ), x * w) print (torch.autograd.grad(mse, [w]))
loss.backward 1 2 3 4 5 x = torch.ones(1 ) w = torch.tensor([2. ], requires_grad=True ) mse = F.mse_loss(torch.ones(1 ), x * w) mse.backward() print (w.grad)
F.softmax
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 a = torch.rand(3 ) a.requires_grad_() p = F.softmax(a, dim=0 ) print (p)dp1 = torch.autograd.grad(p[0 ], [a], retain_graph=True ) print (dp1)dp2 = torch.autograd.grad(p[1 ], [a], retain_graph=True ) print (dp2)dp3 = torch.autograd.grad(p[2 ], [a]) print (dp3)""" tensor([0.3132, 0.3989, 0.2879], grad_fn=<SoftmaxBackward0>) (tensor([ 0.2151, -0.1249, -0.0902]),) (tensor([-0.1249, 0.2398, -0.1148]),) (tensor([-0.0902, -0.1148, 0.2050]),) """
感知机模型 单输出感知机
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 import torchimport torch.nn.functional as Fx = torch.rand(3 , 10 ) w = torch.rand(1 , 10 , requires_grad=True ) o = torch.sigmoid(x @ w.t()) print (o)loss = F.mse_loss(torch.FloatTensor([[1 ], [0 ], [0 ]]), o) loss.backward() print (loss, w.grad)""" tensor([[0.8605], [0.8590], [0.7049]], grad_fn=<SigmoidBackward0>) tensor(0.4181, grad_fn=<MseLossBackward0>) tensor([[0.0851, 0.0223, 0.0701, 0.0971, 0.0574, 0.0612, 0.0456, 0.0683, 0.0352, 0.0944]]) """
多输出感知机
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 import torchimport torch.nn.functional as Fx = torch.rand(3 , 10 ) w = torch.rand(4 , 10 , requires_grad=True ) o = torch.sigmoid(x @ w.t()) print (o)label = torch.FloatTensor([[1 , 0.5 , 0 , 0 ], [0 , 1 , 0.2 , 0 ], [0 , 0 , 0 , 0.8 ]]) loss = F.mse_loss(label, o) loss.backward() print (loss, w.grad)""" tensor([[0.9386, 0.8571, 0.8541, 0.8488], [0.8648, 0.9295, 0.9111, 0.7584], [0.9539, 0.9195, 0.8927, 0.9121]], grad_fn=<SigmoidBackward0>) tensor(0.4983, grad_fn=<MseLossBackward0>) tensor([[0.0148, 0.0137, 0.0151, 0.0075, 0.0186, 0.0043, 0.0097, 0.0156, 0.0149, 0.0040], [0.0121, 0.0009, 0.0118, 0.0055, 0.0073, 0.0137, 0.0102, 0.0102, 0.0065, 0.0134], [0.0260, 0.0099, 0.0312, 0.0133, 0.0204, 0.0245, 0.0174, 0.0205, 0.0177, 0.0251], [0.0245, 0.0193, 0.0359, 0.0143, 0.0252, 0.0165, 0.0110, 0.0180, 0.0216, 0.0185]]) """
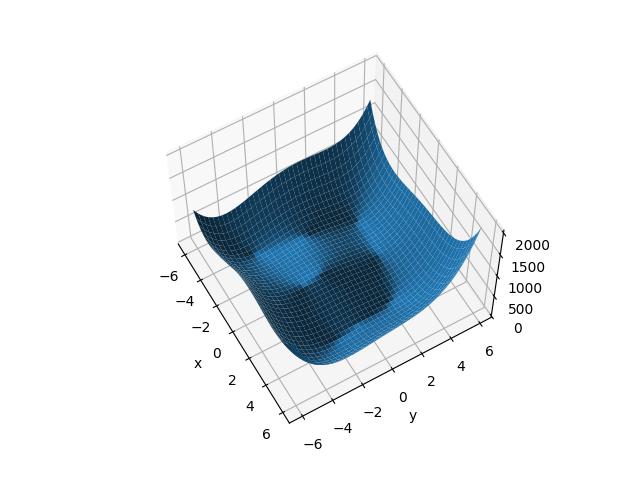
himmelblau函数优化
himmelblau函数是数学家们构造出来的一个特殊的函数,可以用来测试深度学习算法是否能够收敛到局部最小值。这个函数的表达式是:
三维图像展示 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 import numpy as npfrom matplotlib import pyplot as pltimport torchdef himmelblau (x ): return (x[0 ] ** 2 + x[1 ] - 11 ) ** 2 + (x[0 ] + x[1 ] ** 2 - 7 ) ** 2 x = np.arange(-6 , 6 , 0.1 ) y = np.arange(-6 , 6 , 0.1 ) X, Y = np.meshgrid(x, y) Z = himmelblau([X, Y]) fig = plt.figure('himmelblau' ) ax = fig.add_subplot(projection='3d' ) ax.plot_surface(X, Y, Z) ax.view_init(60 , -30 ) ax.set_xlabel('x' ) ax.set_ylabel('y' ) plt.savefig("himmelblau.jpg" ) plt.show()
梯度下降求最小值 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 x = torch.tensor([0. , 4. ], requires_grad=True ) optimizer = torch.optim.Adam([x], lr=1e-3 ) for step in range (20000 ): loss = himmelblau(x) optimizer.zero_grad() loss.backward() optimizer.step() if step % 2000 == 0 : print ('step {}:x={},f(x)={}' .format (step, x.tolist(), loss.item())) """ [0, 4] step 18000:x=[-2.8051180839538574, 3.131312370300293],f(x)=2.2737367544323206e-13 [0,0] step 18000:x=[3.0, 2.0],f(x)=0.0 [-4, 0] step 18000:x=[-3.7793102264404297, -3.2831859588623047],f(x)=0.0 [4, 0] step 18000:x=[3.584428310394287, -1.8481265306472778],f(x)=0.0 """
初始化位置的不同将会影响最终收敛到哪个局部最小值
交叉熵 $$
衡量两个分布p和q的不一致程度,在分类问题中可用于衡量损失。
F.cross_entropy 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 import torchimport torch.nn.functional as Fx = torch.randn(1 , 784 ) w = torch.randn(10 , 784 ) label = torch.tensor([3 ]) print (label)logits = x @ w.t() print (logits)pred = F.softmax(logits, dim=1 ) pred_log = torch.log(pred) loss = F.nll_loss(pred_log, label) print (loss)cross_en = F.cross_entropy(logits, label) print (cross_en)
多分类问题 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 import torchimport torch.nn as nnimport torch.nn.functional as Fimport torch.optim as optimfrom torchvision import datasets, transformsbatch_size = 200 learning_rate = 0.01 epochs = 10 train_loader = torch.utils.data.DataLoader( datasets.MNIST('../data' , train=True , download=True , transform=transforms.Compose([ transforms.ToTensor(), transforms.Normalize((0.1307 ,), (0.3081 ,)) ])), batch_size=batch_size, shuffle=True ) test_loader = torch.utils.data.DataLoader( datasets.MNIST('../data' , train=False , transform=transforms.Compose([ transforms.ToTensor(), transforms.Normalize((0.1307 ,), (0.3081 ,)) ])), batch_size=batch_size, shuffle=True )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 w1, b1 = torch.randn(200 , 784 , requires_grad=True ), \ torch.zeros(200 , requires_grad=True ) w2, b2 = torch.randn(200 , 200 , requires_grad=True ), \ torch.zeros(200 , requires_grad=True ) w3, b3 = torch.randn(10 , 200 , requires_grad=True ), \ torch.zeros(10 , requires_grad=True ) torch.nn.init.kaiming_normal_(w1) torch.nn.init.kaiming_normal_(w2) torch.nn.init.kaiming_normal_(w3) def forward (x ): x = x @ w1.t() + b1 x = F.relu(x) x = x @ w2.t() + b2 x = F.relu(x) x = x @ w3.t() + b3 x = F.relu(x) return x optimizer = optim.SGD([w1, b1, w2, b2, w3, b3], lr=learning_rate) criteon = nn.CrossEntropyLoss() for epoch in range (epochs): for batch_idx, (data, target) in enumerate (train_loader): data = data.view(-1 , 28 * 28 ) logits = forward(data) loss = criteon(logits, target) optimizer.zero_grad() loss.backward() optimizer.step() if batch_idx % 100 == 0 : print ('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}' .format ( epoch, batch_idx * len (data), len (train_loader.dataset), 100. * batch_idx / len (train_loader), loss.item())) test_loss = 0 correct = 0 for data, target in test_loader: data = data.view(-1 , 28 * 28 ) logits = forward(data) test_loss += criteon(logits, target).item() pred = logits.data.max (1 )[1 ] correct += pred.eq(target.data).sum () test_loss /= len (test_loader.dataset) print ('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n' .format ( test_loss, correct, len (test_loader.dataset), 100. * correct / len (test_loader.dataset)))
全连接神经网络 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 import torchimport torch.nn as nnimport torch.optim as optimfrom torchvision import datasets, transformsbatch_size = 200 learning_rate = 0.01 epochs = 10 train_loader = torch.utils.data.DataLoader( datasets.MNIST('../data' , train=True , download=True , transform=transforms.Compose([ transforms.ToTensor(), transforms.Normalize((0.1307 ,), (0.3081 ,)) ])), batch_size=batch_size, shuffle=True ) test_loader = torch.utils.data.DataLoader( datasets.MNIST('../data' , train=False , transform=transforms.Compose([ transforms.ToTensor(), transforms.Normalize((0.1307 ,), (0.3081 ,)) ])), batch_size=batch_size, shuffle=True )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 class MLP (nn.Module ): def __init__ (self ): """初始化模型网络层""" super (MLP, self).__init__() self.model = nn.Sequential( nn.Linear(784 , 200 ), nn.ReLU(inplace=True ), nn.Linear(200 , 200 ), nn.ReLU(inplace=True ), nn.Linear(200 , 10 ), nn.ReLU(inplace=True ), ) def forward (self, x ): """前向传播""" x = self.model(x) return x net = MLP() optimizer = optim.SGD(net.parameters(), lr=learning_rate) criteon = nn.CrossEntropyLoss() for epoch in range (epochs): for batch_idx, (data, target) in enumerate (train_loader): data = data.view(-1 , 28 * 28 ) logits = net(data) loss = criteon(logits, target) optimizer.zero_grad() loss.backward() optimizer.step() if batch_idx % 100 == 0 : print ('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}' .format ( epoch, batch_idx * len (data), len (train_loader.dataset), 100. * batch_idx / len (train_loader), loss.item())) test_loss = 0 correct = 0 for data, target in test_loader: data = data.view(-1 , 28 * 28 ) logits = net(data) test_loss += criteon(logits, target).item() pred = logits.data.max (1 )[1 ] correct += pred.eq(target.data).sum () test_loss /= len (test_loader.dataset) print ('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n' .format ( test_loss, correct, len (test_loader.dataset), 100. * correct / len (test_loader.dataset)))
激活函数与CPU加速 激活函数
tanh,sigmoid
relu
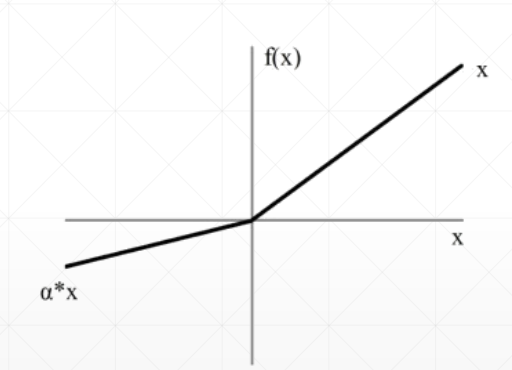
leak relu
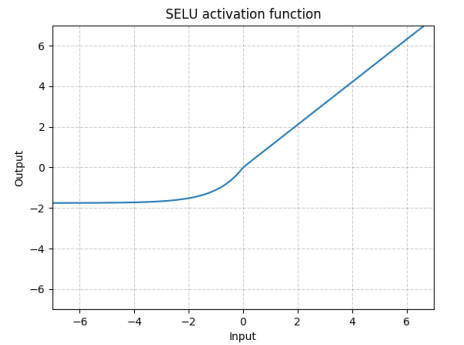
selu
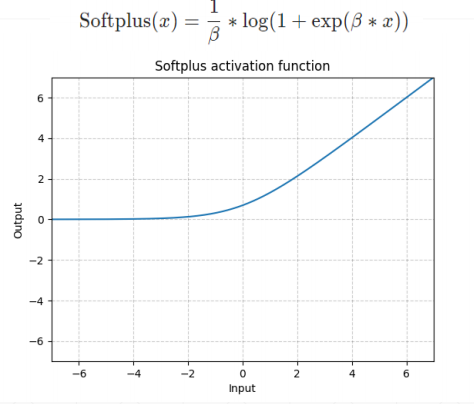
softplus
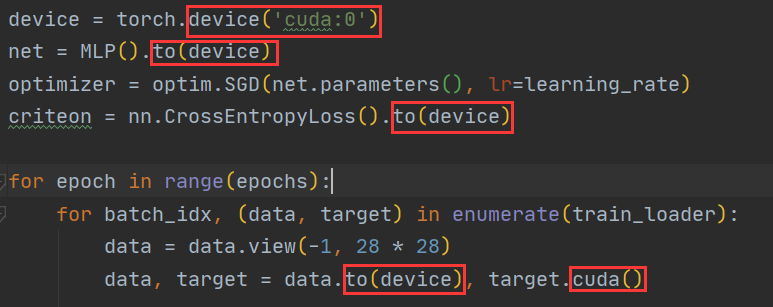
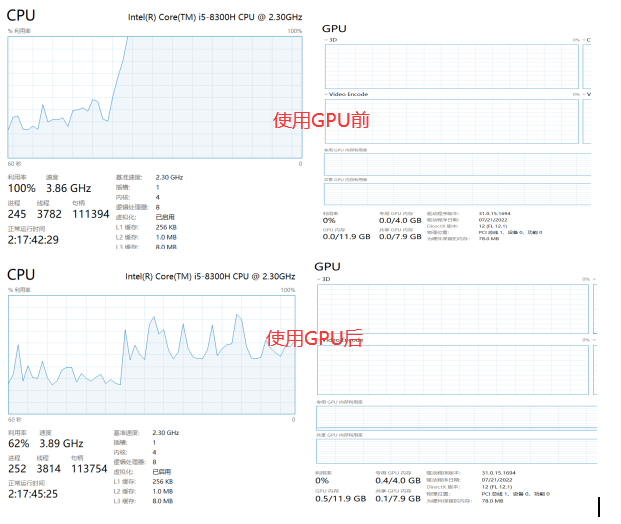
CPU加速
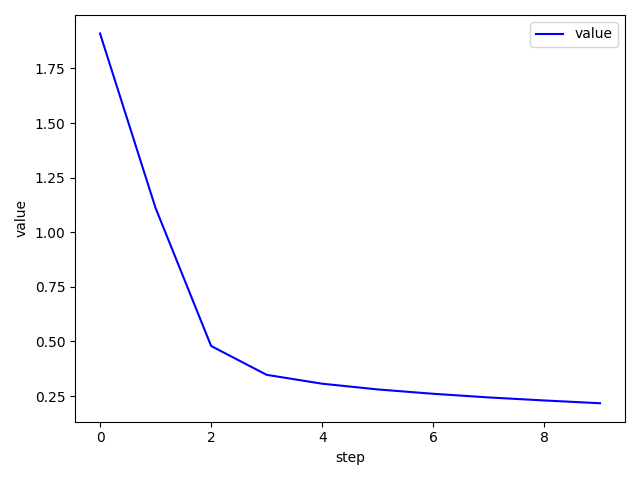
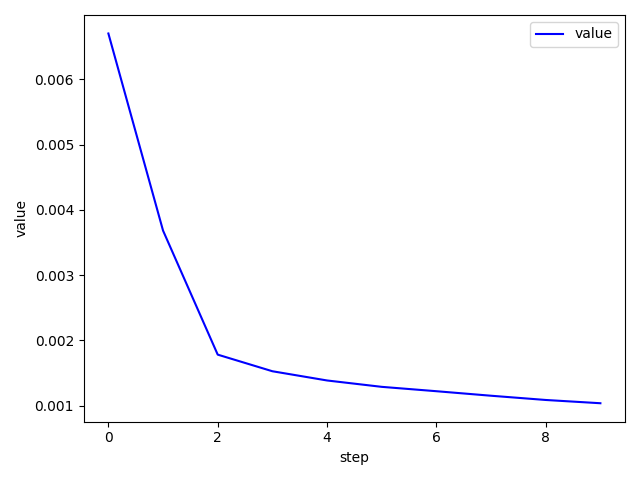
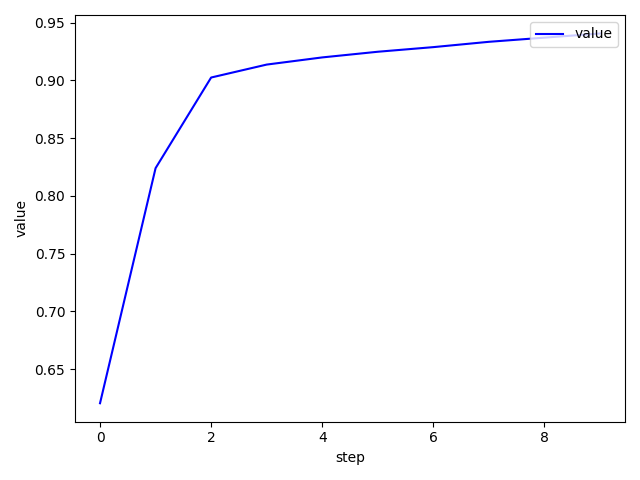
手写体数字识别 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 import torchimport torch.nn as nnimport torch.nn.functional as Fimport torch.optim as optimfrom torchvision import datasets, transformsfrom plot.utils import plot_image, plot_curvebatch_size = 200 learning_rate = 0.01 epochs = 10 train_loader = torch.utils.data.DataLoader( datasets.MNIST('../data' , train=True , download=True , transform=transforms.Compose([ transforms.ToTensor(), transforms.Normalize((0.1307 ,), (0.3081 ,)) ])), batch_size=batch_size, shuffle=True ) test_loader = torch.utils.data.DataLoader( datasets.MNIST('../data' , train=False , transform=transforms.Compose([ transforms.ToTensor(), transforms.Normalize((0.1307 ,), (0.3081 ,)) ])), batch_size=batch_size, shuffle=True ) x, y = next (iter (train_loader)) print (x.shape, y.shape, x.min (), x.max ())plot_image(x, y, 'image sample' ) class MLP (nn.Module ): def __init__ (self ): super (MLP, self).__init__() self.model = nn.Sequential( nn.Linear(784 , 200 ), nn.LeakyReLU(inplace=True ), nn.Linear(200 , 200 ), nn.LeakyReLU(inplace=True ), nn.Linear(200 , 10 ), nn.LeakyReLU(inplace=True ), ) def forward (self, x ): x = self.model(x) return x device = torch.device('cuda:0' ) net = MLP().to(device) optimizer = optim.SGD(net.parameters(), lr=learning_rate) criteon = nn.CrossEntropyLoss().to(device) train_losses = [] test_losses = [] accuracys = [] for epoch in range (epochs): for batch_idx, (data, target) in enumerate (train_loader): data = data.view(-1 , 28 * 28 ) data, target = data.to(device), target.cuda() logits = net(data) loss = criteon(logits, target) optimizer.zero_grad() loss.backward() optimizer.step() train_losses.append(loss.item()) if batch_idx % 100 == 0 : print ('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}' .format ( epoch, batch_idx * len (data), len (train_loader.dataset), 100. * batch_idx / len (train_loader), loss.item())) test_loss = 0 correct = 0 for data, target in test_loader: data = data.view(-1 , 28 * 28 ) data, target = data.to(device), target.cuda() logits = net(data) test_loss += criteon(logits, target).item() pred = logits.argmax(dim=1 ) correct += pred.eq(target).float ().sum ().item() test_loss /= len (test_loader.dataset) test_losses.append(test_loss) accuracys.append(correct / len (test_loader.dataset)) print ('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n' .format ( test_loss, correct, len (test_loader.dataset), 100. * correct / len (test_loader.dataset))) plot_curve(train_losses) plot_curve(test_losses) plot_curve(accuracys)
plot.utils
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 import torchfrom matplotlib import pyplot as pltdef plot_curve (data ): fig = plt.figure() plt.plot(range (len (data)), data, color='blue' ) plt.legend(['value' ], loc='upper right' ) plt.xlabel('step' ) plt.ylabel('value' ) plt.show() def plot_image (img, label, name ): fig = plt.figure() for i in range (6 ): plt.subplot(2 , 3 , i + 1 ) plt.tight_layout() plt.imshow(img[i][0 ] * 0.3081 + 0.1307 , cmap='gray' , interpolation='none' ) plt.title("{}: {}" .format (name, label[i].item())) plt.xticks([]) plt.yticks([]) plt.show() def one_hot (label, depth=10 ): out = torch.zeros(label.size(0 ), depth) idx = torch.LongTensor(label).view(-1 , 1 ) out.scatter_(dim=1 , index=idx, value=1 ) return out
visdom可视化 安装与启动
step1 安装
1 2 3 pip install visdom pip install visdom -i https://pypi.tuna.tsinghua.edu.cn/simple
step2 启动
问题解决可参考
作图举例
实时绘制损失和精度
1 2 3 4 5 6 7 8 9 10 11 from visdom import Visdomviz = visdom.Visdom(env='mnist' ) viz.line([0. ], [0. ], win='train_loss' , opts=dict (title='train loss' )) viz.line([0. ], [0. ], win='acc' , opts=dict (title='test acc' )) viz.line([loss.item()], [global_step], win='train_loss' , update='append' )
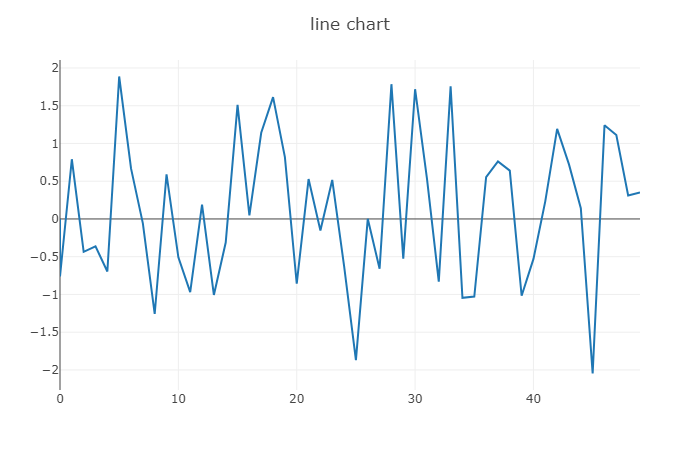
绘制折线图
1 2 3 4 5 6 7 8 9 10 11  viz.line([0. ], [0. ], win='line' , opts=dict (title='line chart' )) a, b = 0 , 0 for i in range (50 ): a = np.array([i]) b = np.random.randn(1 ) viz.line(b, a, win='line' , update="append" )
绘制Image图像
1 2 3 4 viz = Visdom(env="images" ) viz.images(torch.randn(16 , 3 , 32 , 32 ).numpy(), nrow=4 , win='imgs' , opts={'title' : 'imgs' })
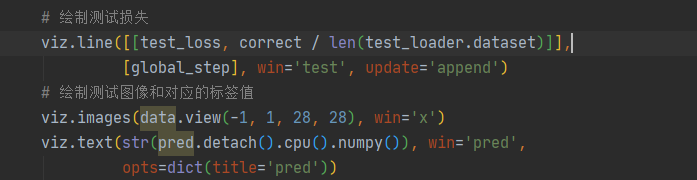
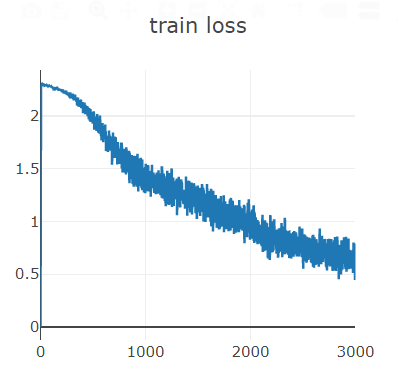
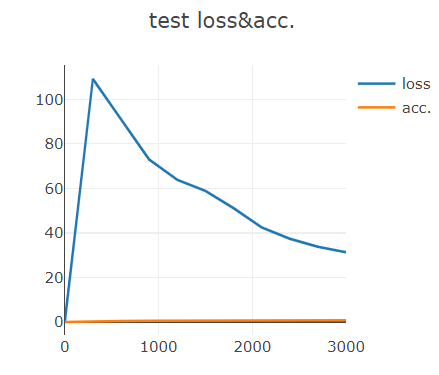
与pytorch联用 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 import torchimport torch.nn as nnimport torch.nn.functional as Fimport torch.optim as optimfrom torchvision import datasets, transformsfrom visdom import Visdombatch_size = 200 learning_rate = 0.01 epochs = 10 train_loader = torch.utils.data.DataLoader( datasets.MNIST('../data' , train=True , download=True , transform=transforms.Compose([ transforms.ToTensor(), ])), batch_size=batch_size, shuffle=True ) test_loader = torch.utils.data.DataLoader( datasets.MNIST('../data' , train=False , transform=transforms.Compose([ transforms.ToTensor(), ])), batch_size=batch_size, shuffle=True ) class MLP (nn.Module ): def __init__ (self ): super (MLP, self).__init__() self.model = nn.Sequential( nn.Linear(784 , 200 ), nn.LeakyReLU(inplace=True ), nn.Linear(200 , 200 ), nn.LeakyReLU(inplace=True ), nn.Linear(200 , 10 ), nn.LeakyReLU(inplace=True ), ) def forward (self, x ): x = self.model(x) return x device = torch.device('cuda:0' ) net = MLP().to(device) optimizer = optim.SGD(net.parameters(), lr=learning_rate) criteon = nn.CrossEntropyLoss().to(device) viz = Visdom() viz.line([0. ], [0. ], win='train_loss' , opts=dict (title='train loss' )) viz.line([[0.0 , 0.0 ]], [0. ], win='test' , opts=dict (title='test loss&acc.' , legend=['loss' , 'acc.' ])) global_step = 0 for epoch in range (epochs): for batch_idx, (data, target) in enumerate (train_loader): data = data.view(-1 , 28 * 28 ) data, target = data.to(device), target.cuda() logits = net(data) loss = criteon(logits, target) optimizer.zero_grad() loss.backward() optimizer.step() global_step += 1 viz.line([loss.item()], [global_step], win='train_loss' , update='append' ) if batch_idx % 100 == 0 : print ('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}' .format ( epoch, batch_idx * len (data), len (train_loader.dataset), 100. * batch_idx / len (train_loader), loss.item())) test_loss = 0 correct = 0 for data, target in test_loader: data = data.view(-1 , 28 * 28 ) data, target = data.to(device), target.cuda() logits = net(data) test_loss += criteon(logits, target).item() pred = logits.argmax(dim=1 ) correct += pred.eq(target).float ().sum ().item() viz.line([[test_loss, correct / len (test_loader.dataset)]], [global_step], win='test' , update='append' ) viz.images(data.view(-1 , 1 , 28 , 28 ), win='x' ) viz.text(str (pred.detach().cpu().numpy()), win='pred' , opts=dict (title='pred' )) test_loss /= len (test_loader.dataset) print ('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n' .format ( test_loss, correct, len (test_loader.dataset), 100. * correct / len (test_loader.dataset)))
交叉验证 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 import torchimport torch.nn as nnimport torch.nn.functional as Fimport torch.optim as optimfrom torchvision import datasets, transformsfrom visdom import Visdombatch_size = 200 learning_rate = 0.01 epochs = 10 train_db = datasets.MNIST('../data' , train=True , download=True , transform=transforms.Compose([ transforms.ToTensor(), transforms.Normalize((0.1307 ,), (0.3081 ,)) ])) train_loader = torch.utils.data.DataLoader( train_db, batch_size=batch_size, shuffle=True ) test_db = datasets.MNIST('../data' , train=False , transform=transforms.Compose([ transforms.ToTensor(), transforms.Normalize((0.1307 ,), (0.3081 ,)) ])) test_loader = torch.utils.data.DataLoader(test_db, batch_size=batch_size, shuffle=True ) print ('train:' , len (train_db), 'test:' , len (test_db))train_db, val_db = torch.utils.data.random_split(train_db, [50000 , 10000 ]) print ('db1:' , len (train_db), 'db2:' , len (val_db))train_loader = torch.utils.data.DataLoader( train_db, batch_size=batch_size, shuffle=True ) val_loader = torch.utils.data.DataLoader( val_db, batch_size=batch_size, shuffle=True ) class MLP (nn.Module ): def __init__ (self ): super (MLP, self).__init__() self.model = nn.Sequential( nn.Linear(784 , 200 ), nn.LeakyReLU(inplace=True ), nn.Linear(200 , 200 ), nn.LeakyReLU(inplace=True ), nn.Linear(200 , 10 ), nn.LeakyReLU(inplace=True ), ) def forward (self, x ): x = self.model(x) return x device = torch.device('cuda:0' ) net = MLP().to(device) optimizer = optim.SGD(net.parameters(), lr=learning_rate) criteon = nn.CrossEntropyLoss().to(device) viz = Visdom(env='cross validation' ) viz.line([0. ], [0. ], win='train_loss' , opts=dict (title='train loss' )) viz.line([[0.0 , 0.0 ]], [0. ], win='val' , opts=dict (title='validation loss&acc.' , legend=['loss' , 'acc.' ])) global_step = 0 for epoch in range (epochs): for batch_idx, (data, target) in enumerate (train_loader): data = data.view(-1 , 28 * 28 ) data, target = data.to(device), target.cuda() logits = net(data) loss = criteon(logits, target) optimizer.zero_grad() loss.backward() optimizer.step() global_step += 1 viz.line([loss.item()], [global_step], win='train_loss' , update='append' ) if batch_idx % 100 == 0 : print ('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}' .format ( epoch, batch_idx * len (data), len (train_loader.dataset), 100. * batch_idx / len (train_loader), loss.item())) val_loss = 0 correct = 0 for data, target in val_loader: data = data.view(-1 , 28 * 28 ) data, target = data.to(device), target.cuda() logits = net(data) val_loss += criteon(logits, target).item() pred = logits.argmax(dim=1 ) correct += pred.eq(target.data).sum ().item() viz.line([[val_loss, correct / len (test_loader.dataset)]], [global_step], win='val' , update='append' ) val_loss /= len (val_loader.dataset) print ('\nVAL set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n' .format ( val_loss, correct, len (val_loader.dataset), 100. * correct / len (val_loader.dataset))) test_loss = 0 correct = 0 for data, target in test_loader: data = data.view(-1 , 28 * 28 ) data, target = data.to(device), target.cuda() logits = net(data) test_loss += criteon(logits, target).item() pred = logits.data.max (1 )[1 ] correct += pred.eq(target.data).sum () test_loss /= len (test_loader.dataset) print ('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n' .format ( test_loss, correct, len (test_loader.dataset), 100. * correct / len (test_loader.dataset)))
划分数据集 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 train_db = datasets.MNIST('../data' , train=True , download=True , transform=transforms.Compose([ transforms.ToTensor(), transforms.Normalize((0.1307 ,), (0.3081 ,)) ])) train_loader = torch.utils.data.DataLoader( train_db, batch_size=batch_size, shuffle=True ) test_db = datasets.MNIST('../data' , train=False , transform=transforms.Compose([ transforms.ToTensor(), transforms.Normalize((0.1307 ,), (0.3081 ,)) ])) test_loader = torch.utils.data.DataLoader(test_db, batch_size=batch_size, shuffle=True ) print ('train:' , len (train_db), 'test:' , len (test_db))train_db, val_db = torch.utils.data.random_split(train_db, [50000 , 10000 ]) print ('db1:' , len (train_db), 'db2:' , len (val_db))train_loader = torch.utils.data.DataLoader( train_db, batch_size=batch_size, shuffle=True ) val_loader = torch.utils.data.DataLoader( val_db, batch_size=batch_size, shuffle=True )
k-fold cross-validation pytorch - K折交叉验证过程说明及实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 import torchimport torch.nn as nnfrom torch.utils.data import DataLoader,Dataset import torch.nn.functional as Ffrom torch.autograd import Variable x = torch.rand(100 ,28 ,28 ) y = torch.randn(100 ,28 ,28 ) x = torch.cat((x,y),dim=0 ) label =[1 ] *100 + [0 ]*100 label = torch.tensor(label,dtype=torch.long) class Net (nn.Module ): def __init__ (self ): super (Net, self).__init__() self.fc1 = nn.Linear(28 *28 , 120 ) self.fc2 = nn.Linear(120 , 84 ) self.fc3 = nn.Linear(84 , 2 ) def forward (self, x ): x = x.view(-1 , self.num_flat_features(x)) x = F.relu(self.fc1(x)) x = F.relu(self.fc2(x)) x = self.fc3(x) return x def num_flat_features (self, x ): size = x.size()[1 :] num_features = 1 for s in size: num_features *= s return num_features class TraindataSet (Dataset ): def __init__ (self,train_features,train_labels ): self.x_data = train_features self.y_data = train_labels self.len = len (train_labels) def __getitem__ (self,index ): return self.x_data[index],self.y_data[index] def __len__ (self ): return self.len def get_k_fold_data (k, i, X, y ): assert k > 1 fold_size = X.shape[0 ] // k X_train, y_train = None , None for j in range (k): idx = slice (j * fold_size, (j + 1 ) * fold_size) X_part, y_part = X[idx, :], y[idx] if j == i: X_valid, y_valid = X_part, y_part elif X_train is None : X_train, y_train = X_part, y_part else : X_train = torch.cat((X_train, X_part), dim=0 ) y_train = torch.cat((y_train, y_part), dim=0 ) return X_train, y_train, X_valid,y_valid def k_fold (k, X_train, y_train, num_epochs=3 ,learning_rate=0.001 , weight_decay=0.1 , batch_size=5 ): train_loss_sum, valid_loss_sum = 0 , 0 train_acc_sum ,valid_acc_sum = 0 ,0 for i in range (k): data = get_k_fold_data(k, i, X_train, y_train) net = Net() train_ls, valid_ls = train(net, *data, num_epochs, learning_rate,\ weight_decay, batch_size) print ('*' *25 ,'第' ,i+1 ,'折' ,'*' *25 ) print ('train_loss:%.6f' %train_ls[-1 ][0 ],'train_acc:%.4f\n' %valid_ls[-1 ][1 ],\ 'valid loss:%.6f' %valid_ls[-1 ][0 ],'valid_acc:%.4f' %valid_ls[-1 ][1 ]) train_loss_sum += train_ls[-1 ][0 ] valid_loss_sum += valid_ls[-1 ][0 ] train_acc_sum += train_ls[-1 ][1 ] valid_acc_sum += valid_ls[-1 ][1 ] print ('#' *10 ,'最终k折交叉验证结果' ,'#' *10 ) print ('train_loss_sum:%.4f' %(train_loss_sum/k),'train_acc_sum:%.4f\n' %(train_acc_sum/k),\ 'valid_loss_sum:%.4f' %(valid_loss_sum/k),'valid_acc_sum:%.4f' %(valid_acc_sum/k)) def train (net, train_features, train_labels, test_features, test_labels, num_epochs, learning_rate,weight_decay, batch_size ): train_ls, test_ls = [], [] dataset = TraindataSet(train_features, train_labels) train_iter = DataLoader(dataset, batch_size, shuffle=True ) optimizer = torch.optim.Adam(params=net.parameters(), lr= learning_rate, weight_decay=weight_decay) for epoch in range (num_epochs): for X, y in train_iter: output = net(X) loss = loss_func(output,y) optimizer.zero_grad() loss.backward() optimizer.step() train_ls.append(log_rmse(0 ,net, train_features, train_labels)) if test_labels is not None : test_ls.append(log_rmse(1 ,net, test_features, test_labels)) return train_ls, test_ls def log_rmse (flag,net,x,y ): if flag == 1 : net.eval () output = net(x) result = torch.max (output,1 )[1 ].view(y.size()) corrects = (result.data == y.data).sum ().item() accuracy = corrects*100.0 /len (y) loss = loss_func(output,y) net.train() return (loss.data.item(),accuracy) loss_func = nn.CrossEntropyLoss() k_fold(10 ,x,label)
正则化 奥卡姆剃刀原则 奥卡姆剃刀原则
减少过拟合
More data
Constraint model complexity
shallow
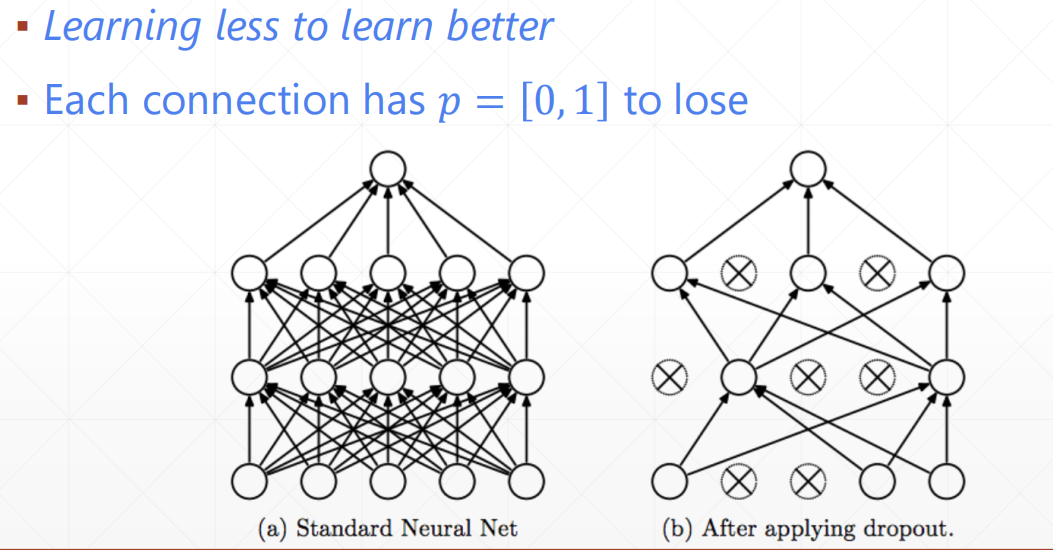
regularization 正则化
Dropput
Data argumentation 数据增强
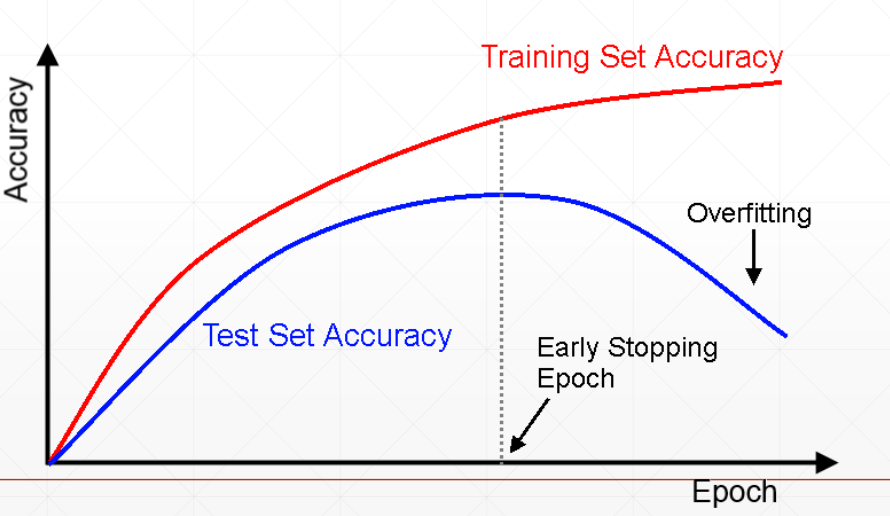
Early stopptin
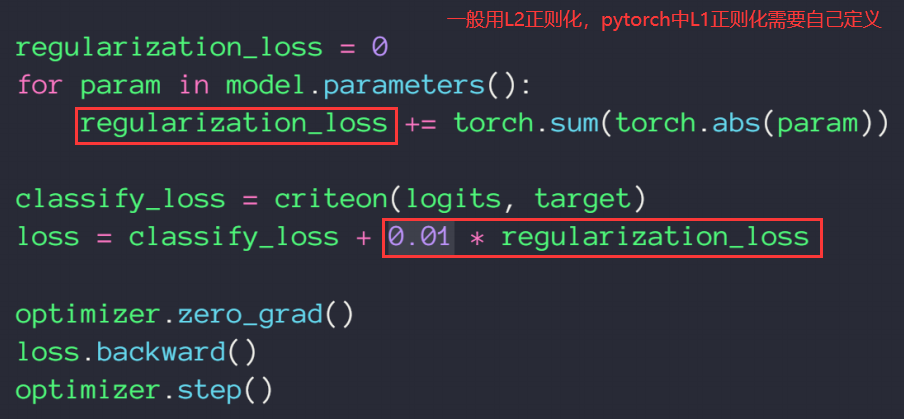
正则化项
实现
L2-regularization
L1-regularization
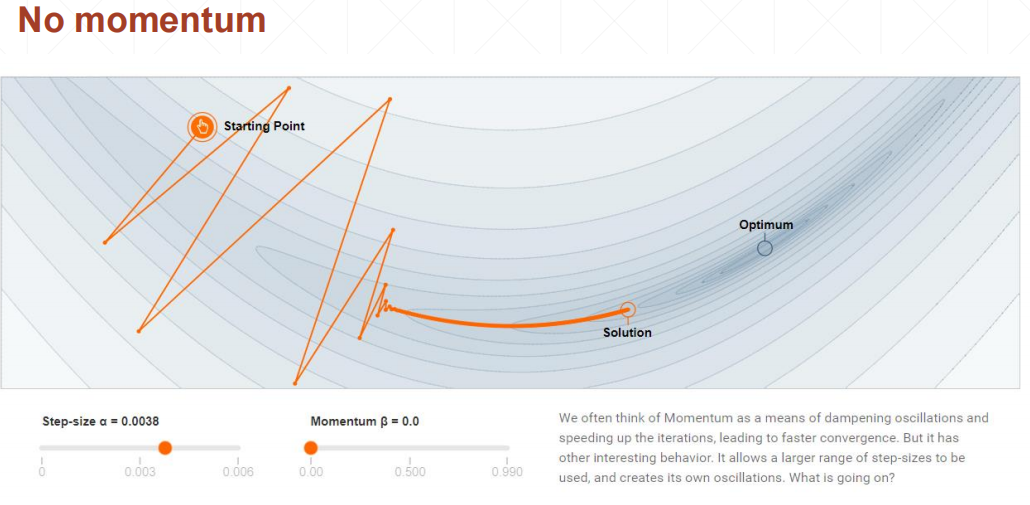
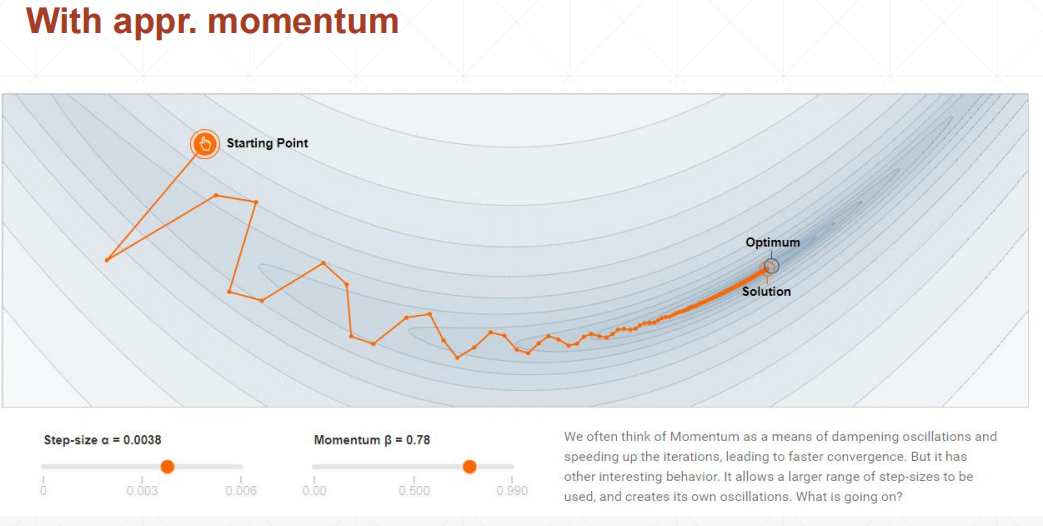
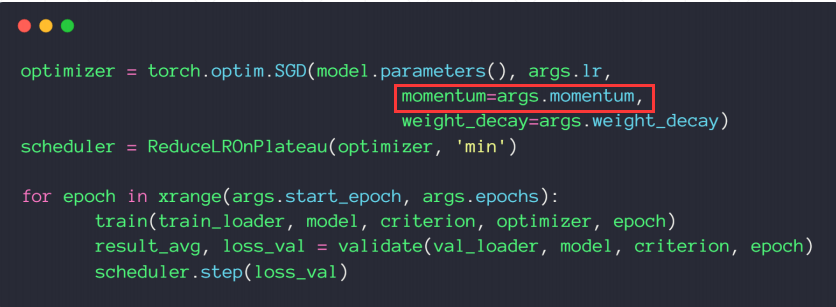
动量和学习率衰减 动量 momentum
也就是说,权值w现在不只向着 $\bigtriangledown{f}$ 的方向衰减,也向着的$z^{k}$方向进行衰减。而$z^{k}$是由$\bigtriangledown{w^{k-1}}$推出的,也就是现在w更新是当前衰减方向和之前衰减方向的惯性的结合。
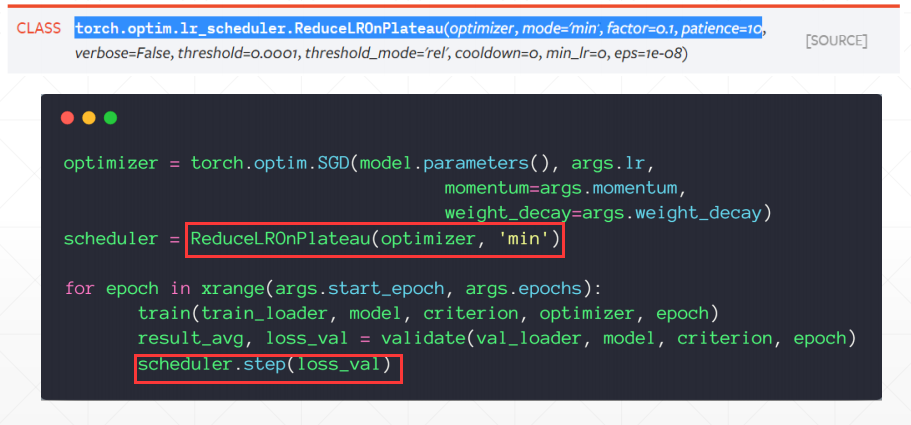
学习率衰减 learning rate decay (1) 第一种,观测loss,如果到了一定时间,一直不变,就代表它无法找到更细分的地方,然后把learning rate减小点。
.step(loss_val)用来监测记录loss,检测周期为patience=的次数,如果没有不变的情况,则只有记录的作用,如果检测到,那么会按设定的规则进行减小learning rate。
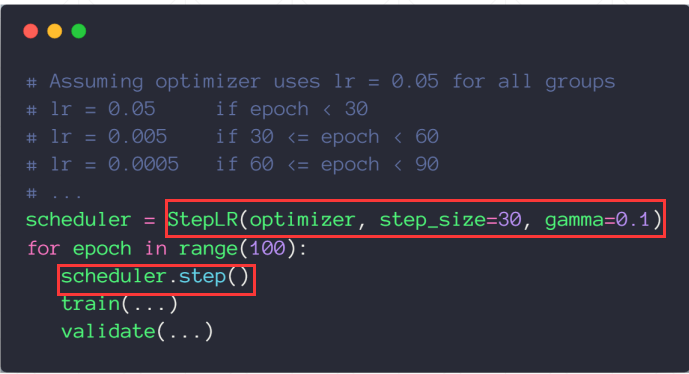
(2) 第二种是简单粗暴的,直接每多少次epoch减小多少
Early stop and Dropout Early stop
Dropput
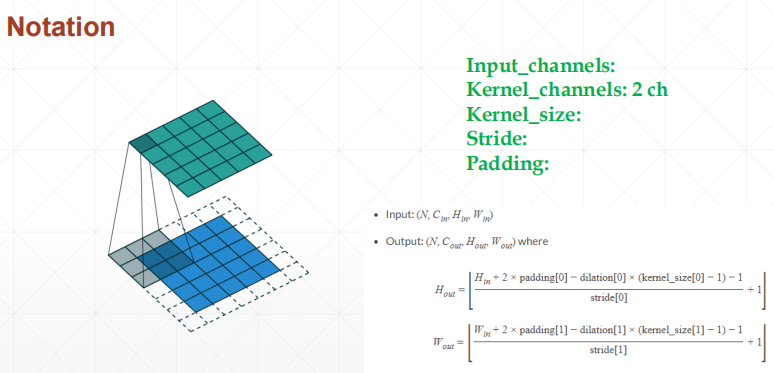
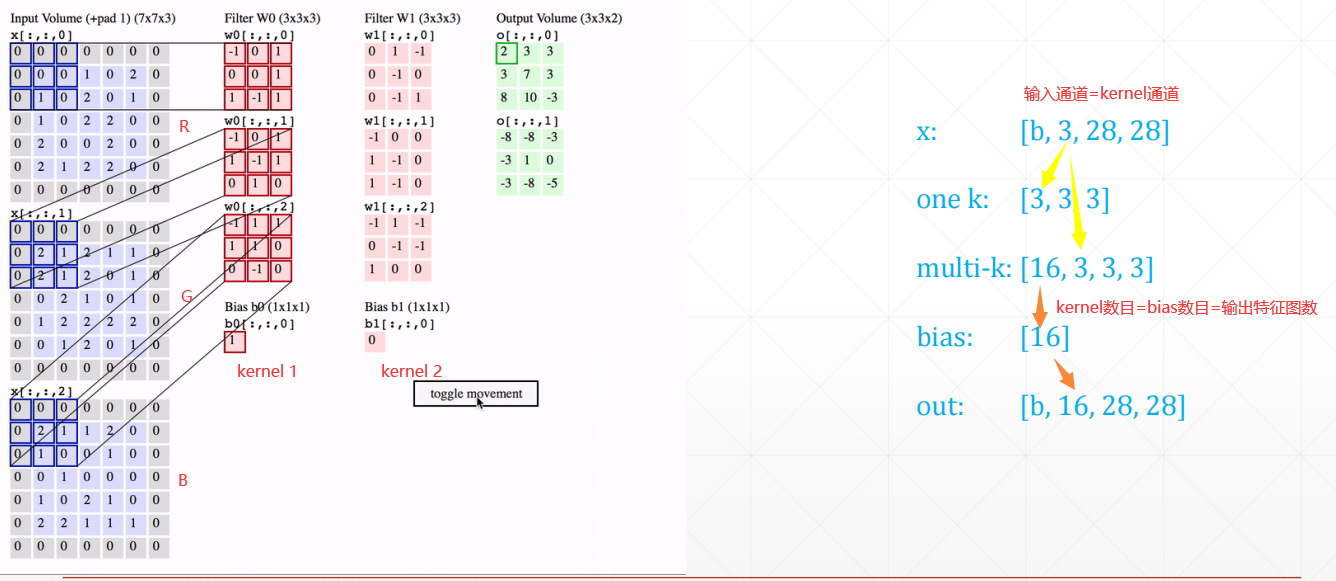
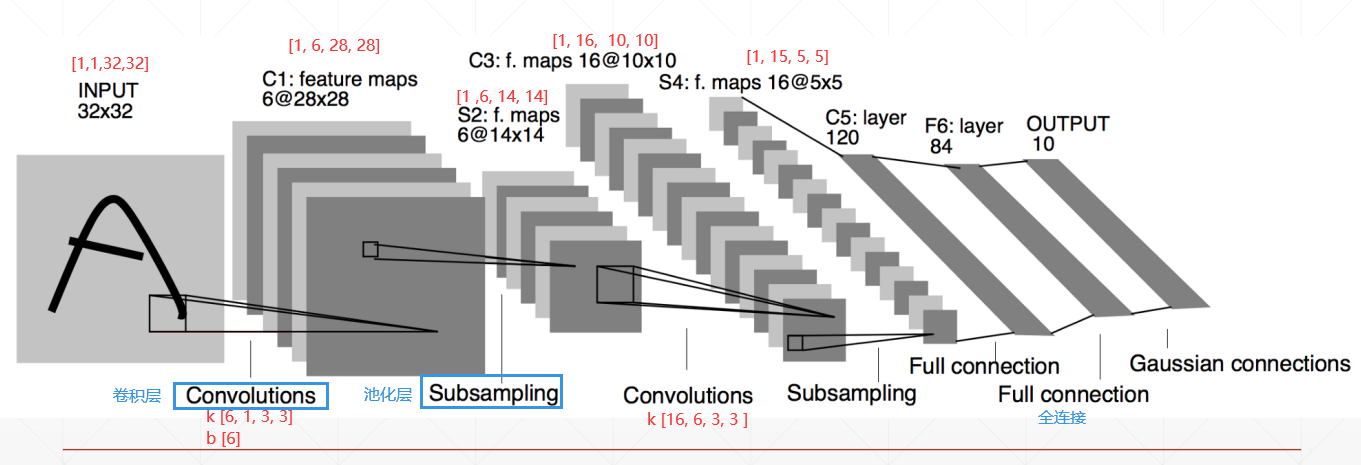
卷积神经网络(CNN) 几个符号含义
Input_channels: 输入数据的通道数,一般是RGB三个通道**Kernel_channels: **Kernel的通道数,与 Input_channels一致, 也是每个kernel里面的卷积数
Kernel_number: Kernel的数目,根据需要自定义Kernel_size: 卷积的尺寸,如3*3Stride: 步长Padding: 补丁
卷积层 nn.Conv2d 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 import torchimport torch.nn as nnimport torch.nn.functional as Fx = torch.rand(1 , 3 , 28 , 28 ) layer = nn.Conv2d(in_channels=3 , out_channels=4 , kernel_size=3 , stride=1 , padding=0 ) out = layer.forward(x) print (out.shape) layer = nn.Conv2d(in_channels=3 , out_channels=4 , kernel_size=3 , stride=1 , padding=1 ) out = layer.forward(x) print (out.shape) layer = nn.Conv2d(in_channels=3 , out_channels=4 , kernel_size=3 , stride=2 , padding=1 ) out = layer.forward(x) print (out.shape) print (layer.weight.shape) print (layer.bias.shape)
F.Conv2d 1 2 3 4 5 6 7 x = torch.rand(1 , 3 , 28 , 28 ) w = torch.rand(4 , 3 , 3 , 3 ) b = torch.rand(4 ) out = F.conv2d(x, w, b, stride=1 , padding=0 ) print (out.shape)
池化层 nn.MaxPool2d 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 import torchimport torch.nn as nnimport torch.nn.functional as Fx = torch.rand(1 , 3 , 28 , 28 ) c_layer = nn.Conv2d(in_channels=3 , out_channels=4 , kernel_size=3 , stride=1 , padding=0 ) out1 = c_layer.forward(x) print (out1.shape) p_layer = nn.MaxPool2d(2 , stride=2 ) out2 = p_layer(out1) print (out2.shape) p_layer = nn.AvgPool2d(2 , stride=2 ) out2 = p_layer(out1) print (out2.shape)
F.max_pool2d 1 2 3 4 5 out2 = F.max_pool2d(out1, 2 , stride=2 ) print (out2.shape) out2 = F.avg_pool2d(out1, 2 , stride=2 ) print (out2.shape)
F.interpolate 1 2 3 4 x = torch.rand(1 , 3 , 28 , 28 ) out = F.interpolate(x, scale_factor=2 , mode='nearest' ) print (out.shape)
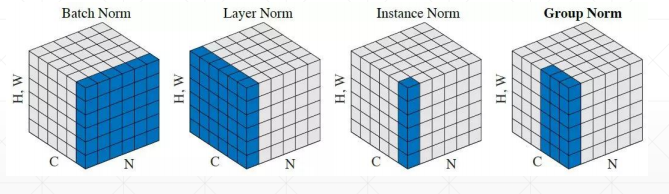
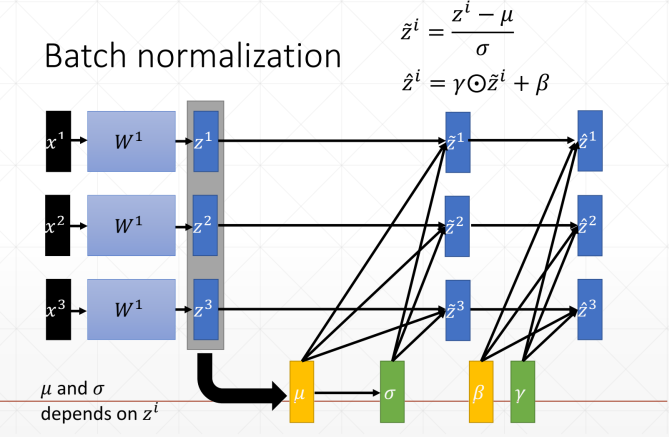
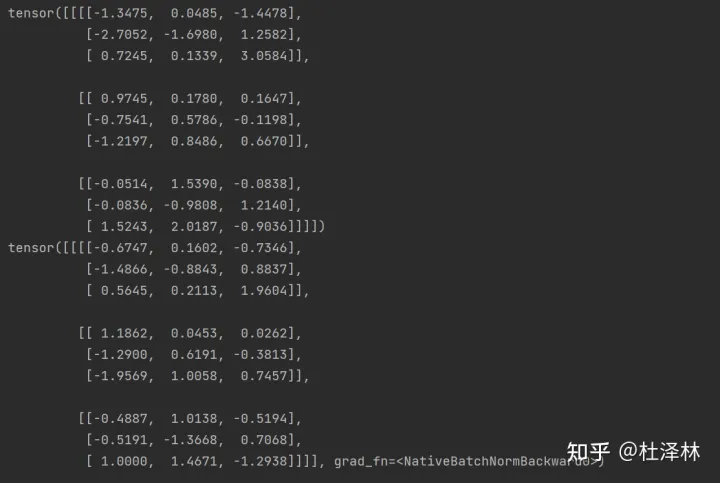
Batch Normalization
优点
Converge faster 收敛更快
Better performance 更好的表现
Robust 鲁棒
nn.Module模块 转载自 pytorch nn.Module模块以及nn部分函数的介绍使用
nn.Module nn.Module是所有神经网络模块的基类,我们使用pytorch构建神经网络需要继承nn.Module类来实现,在__init__构造函数中申明各个层的定义,在forward中实现层之间的连接关系,实际上就是前向传播的过程。
举个栗子,下面是简单构建有一个神经网络:
1 2 3 4 5 6 7 8 9 10 11 12 13 import torch.nn as nnclass Model (nn.Module ): def __init__ (self ): super ().__init__() self.conv1 = nn.Conv2d(1 , 20 , 5 ) self.conv2 = nn.Conv2d(20 , 20 , 5 ) def forward (self, x ): x = nn.ReLU(self.conv1(x)) x = nn.ReLU(self.conv2(x)) return x
nn.Conv2 参数:
1 torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1 , padding=0 , dilation=1 , groups=1 , bias=True , padding_mode='zeros' , device=None , dtype=None )
对由多个输入平面组成的输入信号应用 2D 卷积 。这个就是用在卷积神经网络中的卷积层。
参数
参数类型
in_channels
int
Number of channels in the input image
输入图像通道数
out_channels
int
Number of channels produced by the convolution
卷积产生的通道数
kernel_size
(int or tuple)
Size of the convolving kernel
卷积核尺寸,可以设为1个int型数或者一个(int, int)型的元组。例如(2,3)是高2宽3卷积核
stride
(int or tuple, optional)
Stride of the convolution. Default: 1
卷积步长,默认为1。可以设为1个int型数或者一个(int, int)型的元组。
padding
(int or tuple, optional)
Zero-padding added to both sides of the input. Default: 0
填充操作,控制padding_mode的数目。
padding_mode
(string, optional)
‘zeros’, ‘reflect’, ‘replicate’ or ‘circular’. Default: ‘zeros’
padding模式,默认为Zero-padding 。
dilation
(int or tuple, optional)
Spacing between kernel elements. Default: 1
扩张操作:控制kernel点(卷积核点)的间距,默认值:1。
groups
(int, optional)
Number of blocked connections from input channels to output channels. Default: 1
group参数的作用是控制分组卷积,默认不分组,为1组。
bias
(bool, optional)
If True, adds a learnable bias to the output. Default: True
为真,则在输出中添加一个可学习的偏差。默认:True。
举个栗子:
1 2 3 4 5 6 7 8 9 import torch x = torch.randn(1, 3, 28, 28) print(x.shape) conv2d = torch.nn.Conv2d(in_channels=3, out_channels=12, kernel_size=3) res = conv2d(x) print(res.shape)
nn.MaxPool2d 1 torch.nn.MaxPool2d(kernel_size, stride=None , padding=0 , dilation=1 , return_indices=False , ceil_mode=False )
对由多个输入平面组成的输入信号应用 2D 最大池化 ,用在池化层。Pool层用于提取重要信息的操作,可以去掉部分相邻的信息,减少计算开销。MaxPool在提取数据时,保留相邻信息中的最大值,去掉其他值。
我们先来看一下基本参数,一共六个:
kernel_size :表示做最大池化的窗口大小,可以是单个值,也可以是tuple元组stride :步长,可以是单个值,也可以是tuple元padding :填充,可以是单个值,也可以是tuple元组dilation :控制窗口中元素步幅return_indices :布尔类型,返回最大值位置索引ceil_mode :布尔类型,为True,用向上取整的方法,计算输出形状;默认是向下取整。
举个栗子:
1 2 3 4 5 6 7 8 9 10 import torchx = torch.randn(1 , 3 , 28 , 28 ) print (x.shape)conv2d = torch.nn.Conv2d(in_channels=3 , out_channels=12 , kernel_size=3 ) res = conv2d(x) print (res.shape)pool = torch.nn.MaxPool2d(kernel_size=2 ) res = pool(res) print (res.shape)
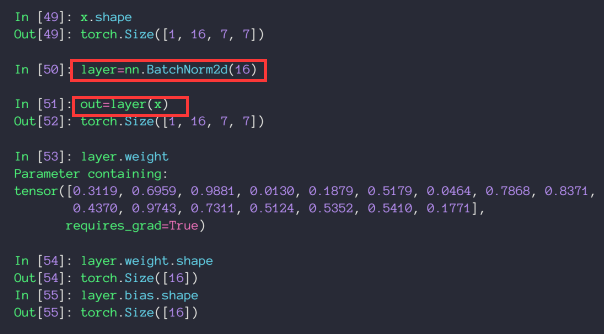
nn.BatchNorm2d 1 torch.nn.BatchNorm2d(num_features, eps=1e-05 , momentum=0.1 , affine=True , track_running_stats=True , device=None , dtype=None )
功能:对输入的四维数组进行批量标准化处理
num_features :输入图像的通道数量。eps :稳定系数,防止分母出现0。momentum : 动态均值和动态方差所使用的动量,即一个用于运行过程中均值和方差的一个估计参数,默认值为0.1。affine :代表gamma,beta是否可学。如果设为True,代表两个参数是通过学习得到的;如果设为False,代表两个参数是固定值,默认情况下,gamma是1,beta是0。track_running_stats :BatchNorm2d中存储的的均值和方差是否需要更新,若为True,表示需要更新;反之不需要更新。
举个栗子:
1 2 3 4 5 6 7 8 import torchm = torch.nn.BatchNorm2d(3 ) input = torch.randn(1 , 3 , 3 , 3 )print (input )output = m(input ) print (output)
nn.Linear nn.Linear()是用于设置网络中的全连接层 的
1 torch.nn.Linear(in_features, out_features, bias=True , device=None , dtype=None )
in_features - 每个输入样本的大小out_features - 每个输出样本的大小bias - 如果设置为False,则图层不会学习附加偏差。默认值:True
1 2 3 4 5 6 7 from torch import nnimport torchm = nn.Linear(3 , 12 ) input = torch.randn(128 , 3 )output = m(input ) print (output.shape)
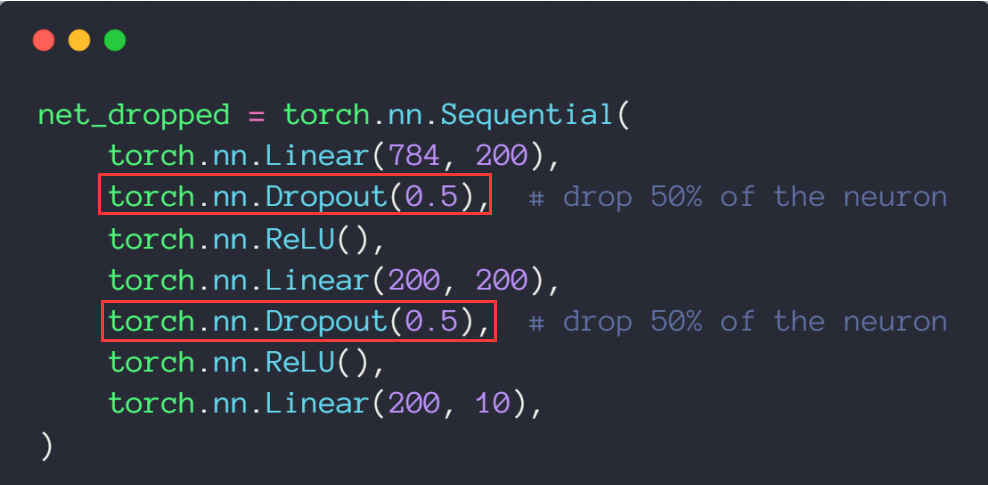
nn.Dropout 在训练期间,使用伯努利分布中的样本,以概率p随机将输入张量的某些元素归零 。
1 torch.nn.Dropout(p=0.5 , inplace=False )
nn.dropout()是为了防止或减轻过拟合 而使用的函数,它一般用在全连接层,Dropout就是在不同的训练过程中随机扔掉一部分神经元。也就是让某个神经元的激活值以一定的概率p,让其停止工作,这次训练过程中不更新权值,也不参加神经网络的计算。但是它的权重得保留下来(只是暂时不更新而已),因为下次样本输入时它可能又得工作了。
nn.ReLU 为了训练深层神经网络,需要一个激活函数神经网络,它看起来和行为都像一个线性函数,但实际上是一个非线性函数,允许学习数据中的复杂关系 。该函数还必须提供更灵敏的激活和输入,避免饱和。
1 torch.nn.ReLU(inplace=False )
nn.Sigmoid Sigmoid 激活函数 ,也被称为 Logistic函数神经网络,传统上是一个非常受欢迎的神经网络激活函数。函数的输入被转换成介于0.0和1.0之间的值。大于1.0的输入被转换为值1.0,同样,小于0.0的值被折断为0.0。所有可能的输入函数的形状都是从0到0.5到1.0的 s 形。
nn.Tanh Tanh的诞生比Sigmoid晚一些,sigmoid函数我们提到过有一个缺点就是输出不以0为中心,使得收敛变慢的问题。而Tanh则就是解决了这个问题。
nn.LSTM LSTM*一般指长短期记忆人工神经网络。 长短期记忆网络 (LSTM ,Long Short-Term Memory)是一种时间循环神经网络,是为了解决一般的RNN(循环神经网络)存在的长期依赖问题而专门设计出来的
1 torch.nn.lstm(input_size,hidden_size,num_layers,bias,batch_first,dropout,bidirectional)
详细介绍一下参数:
input_size :表示的是输入的矩阵特征数,或者说是输入的维度;hidden_size :隐藏层的大小(即隐藏层节点数量),输出向量的维度等于隐藏节点数;num_layer s:lstm 隐层的层数,默认为1;bias :隐层状态是否带 bias,默认为 true;batch_first :True 或者 False,如果是 True,则 input 为(batch, seq, input_size),默认值为:False(seq_len, batch, input_size)dropout :默认值0,除最后一层,每一层的输出都进行dropout;bidirectional :如果设置为 True, 则表示双向 LSTM,默认为 False。
nn.LSTM中输入与输出关系为output, (hn, cn) = lstm(input, (h0, c0)),输入输出格式如下:
1 2 3 4 5 6 7 8 9 input (seq_len, batch, input_size)h0(num_layers * num_directions, batch, hidden_size) c0(num_layers * num_directions, batch, hidden_size) output(seq_len, batch, hidden_size * num_directions) hn(num_layers * num_directions, batch, hidden_size) cn(num_layers * num_directions, batch, hidden_size)
**input (seq_len, batch, input_size)**,seq_len表示每个batch输入多少数据,batch表示把数据分成了batch批,input_size为样本输入维度。
**output(seq_len, batch, hidden_size * num_directions)**,output是一个三维张量,第一维表示序列长度,第二维表示数据批次的多少batch,即数据分为几批送进来,第三维hidden_size隐藏层大小,双向则二倍,单向则等价于隐藏层大小。
hn 是一个三维张量,第一维是num_layers*num_directions,num_layers是我们定义的神经网络的层数,num_directions表示是否为双向LSTM;第二维表示一批的样本数量;第三维表示隐藏层的大小。
c_n与h_n一致。
nn.RNN RNN 一般指循环神经网络。 循环神经网络(Recurrent Neural Network,RNN )是一类以序列(sequence)数据为输入,在序列的演进方向进行递归(recursion)且所有节点(循环单元)按链式连接的递归神经网络(recursive neural network)。
用法同nn.LSTM
nn.GRU 门控循环神经网络(gated recurrent neural network)是为了更好地捕捉时序数据中间隔较大的依赖关系,门控循环单元(gated recurrent unit, GRU)是一种常用的门控循环神经网络。
用法同nn.LSTM
nn.Sequential 一个序列容器,用于搭建神经网络的模块被按照被传入构造器的顺序添加到nn.Sequential()容器 中。
1 2 3 4 5 6 7 8 9 10 11 12 13 from torch import nnimport torchmodel = nn.Sequential( nn.Conv2d(1 , 20 , 5 ), nn.ReLU(), nn.Conv2d(20 , 64 , 5 ), nn.ReLU() ) x = torch.randn(1 , 1 , 30 , 30 ) y = model(x) print (y.shape)
转载自 named_parameters(), named_children, named_modules()方法
named_parameters() 可以对一个nn.Module中所有注册的参数进行迭代:
1 2 3 4 5 6 7 8 9 10 11 import torchfrom torch import nnclass MyLinear (nn.Module ): def __init__ (self, in_features, out_features ): super ().__init__() self.weight = nn.Parameter(torch.randn(in_features, out_features)) self.bias = nn.Parameter(torch.randn(out_features)) def forward (self, input ): return (input @ self.weight) + self.bias
可以通过调用named_parameters()方法得到我们定义的nn.Module, 即MyLinear中所有的可学习的参数:
1 2 3 my_linear = MyLinear(3 , 4 ) for param in my_linear.named_parameters(): print (param)
可以得到以下输出:
1 2 3 4 5 6 ('weight' , Parameter containing: tensor([[ 0.9009 , 0.6984 , 3.0670 , 0.9113 ], [-0.2515 , -0.1617 , 0.2517 , 0.0977 ], [-1.0986 , -0.3517 , -0.4920 , -0.4112 ]], requires_grad=True )) ('bias' , Parameter containing: tensor([-0.2491 , -0.1508 , 0.8393 , -1.3849 ], requires_grad=True ))
我们可以输出更多信息, 来更仔细地查看一下param的内容:
1 2 3 4 5 6 my_linear = MyLinear(3 , 4 ) for param in my_linear.named_parameters(): print (len (param)) print (type (param[0 ]), param[0 ]) print (type (param[1 ]), param[1 ]) break
得到了以下输出:
1 2 3 4 5 6 2 <class 'str '> weight <class 'torch .nn .parameter .Parameter '> Parameter containing : tensor([[-0.3835 , 1.9484 , 0.6865 , -1.0978 ], [-1.7985 , 1.0263 , -0.7779 , -0.4302 ], [-0.2007 , 0.0540 , 0.2876 , 0.0776 ]], requires_grad=True )
可以发现param是由2个元素组成的tuple, 其中第一个元素是str类型的,表示参数的名字, 第二个元素是torch.nn.parameter.Parameter类型的,表示包含的参数信息
named_children() 可以通过调用nn.Module的named_children()方法来查看这个nn.Module的直接子级 的模块:
1 2 3 4 5 6 7 8 9 10 11 12 import torch.nn.functional as Fclass Net (nn.Module ): def __init__ (self ): super ().__init__() self.linear_0 = MyLinear(4 , 3 ) self.linear_1 = MyLinear(3 , 1 ) def forward (self, x ): x = self.linear_0(x) x = F.relu(x) x = self.linear_1(x) return x
这里的Net是由我们定义的MyLinear层组成的, 其中包括了两个children,分别为linear_0和linear_1, 我们使用named_children()可以查看Net所包含的直接子级模块:
1 2 3 net = Net() for child in net.named_children(): print (child)
此时可以得到以下输出:
1 2 ('linear_0' , MyLinear()) ('linear_1' , MyLinear())
如果我们调用了children()方法,与named_children()的区别就是,不会输出名称:
1 2 3 4 5 for child in net.children(): print (child) >>> MyLinear()>>> MyLinear()
named_modules() 在上一个section中我们介绍了named_children(),但是这个方法只能遍历第一级的nn.Module,如果nn.Module()中的直接子级也是一个nn.Module,你需要连着子级一起遍历(going deeper ), 则可以调用named_modules()方法,这个方法会循环遍历nn.Module以及其child nn.Modules ,其实与named_children()的主要区别就是遍历的程度是否更deeper:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 import torch.nn.functional as Fclass Net (nn.Module ): def __init__ (self ): super ().__init__() self.linear_0 = MyLinear(4 , 3 ) self.linear_1 = MyLinear(3 , 1 ) def forward (self, x ): x = self.linear_0(x) x = F.relu(x) x = self.linear_1(x) return x net = Net() for child in net.named_modules(): print (child)
输出的结果如下:
1 2 3 4 5 6 ('' , Net( (linear_0): MyLinear() (linear_1): MyLinear() )) ('linear_0' , MyLinear()) ('linear_1' , MyLinear())
这里可以看到输出了一个Net,是因为named_modules()方法会迭代地找到每个nn.Module,包括自身,我们可以循环打印一下modules()方法的输出的__class__,modules方法与named_modules()的区别就在于是否输出名称:
1 2 3 net = Net() for child in net.modules(): print (child.__class__)
得到以下输出:
1 2 3 <class '__main__ .Net '> <class '__main__ .MyLinear '> <class '__main__ .MyLinear '>
可以看出modules()方法和named_modules()方法会迭代自身
train() and eval() Pytorch 中net.train() 和 net.eval()的作用和如何使用?
net.train()和net.eval()到底在什么时候使用?如果一个模型有Dropout 与BatchNormalization ,那么它在训练时要以一定概率进行Dropout或者更新BatchNormalization参数,而在测试时不在需要Dropout或更新BatchNormalization参数。此时,要用net.train()和net.eval()进行区分。在没有涉及到BN与Dropout的模型,这两个函数没什么用。
save and load
定义自己的Module 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 import torchfrom torch import nnfrom torch import optimclass MyLinear (nn.Module ): def __init__ (self, inp, outp ): super (MyLinear, self).__init__() self.w = nn.Parameter(torch.randn(outp, inp)) self.b = nn.Parameter(torch.randn(outp)) def forward (self, x ): x = x @ self.w.t() + self.b return x class Flatten (nn.Module ): def __init__ (self ): super (Flatten, self).__init__() def forward (self, input ): return input .view(input .size(0 ), -1 ) class TestNet (nn.Module ): def __init__ (self ): super (TestNet, self).__init__() self.net = nn.Sequential(nn.Conv2d(1 , 16 , stride=1 , padding=1 ), nn.MaxPool2d(2 , 2 ), Flatten(), nn.Linear(1 * 14 * 14 , 10 )) def forward (self, x ): return self.net(x) class BasicNet (nn.Module ): def __init__ (self ): super (BasicNet, self).__init__() self.net = nn.Linear(4 , 3 ) def forward (self, x ): return self.net(x) class Net (nn.Module ): def __init__ (self ): super (Net, self).__init__() self.net = nn.Sequential(BasicNet(), nn.ReLU(), nn.Linear(3 , 2 )) def forward (self, x ): return self.net(x) def main (): device = torch.device('cuda' ) net = Net() net.to(device) net.train() net.eval () for name, t in net.named_parameters(): print ('parameters:' , name, t.shape) for name, m in net.named_children(): print ('children:' , name, m) for name, m in net.named_modules(): print ('modules:' , name, m) if __name__ == '__main__' : main()
数据增强 Data argumentation
Flip 翻转
Rotate 旋转
Random Move and Crop 移动,裁剪
Noise 加噪声
GAN
1 2 3 4 5 6 7 8 9 10 11 12 13 train_loader = torch.utils.data.DataLoader( datasets.MNIST('../data' , train=True , download=True , transform=transforms.Compose([ transforms.RandomHorizontalFlip(), transforms.RandomVerticalFlip(), transforms.RandomRotation(15 ), transforms.RandomRotation([90 , 180 , 270 ]), transforms.Resize([32 , 32 ]), transforms.RandomCrop([28 , 28 ]), transforms.ToTensor(), ])), batch_size=batch_size, shuffle=True )