Matlab学习笔记
一、命名规则
- 变量名区分大小写
- 变量名长度不超过63位 (MATLAB R2012a 32bit和64bit计算机上测试结果)
- 变量名以字母开头,可以由字母、数字和下划线组成,但不能使用标点
- 变量名应简洁明了,通过变量名可以直观看出变量所表示的物理意义
- clear all:除Workspace中所有的变量
- clc :清除Command Window中的所有命令
- 注释:%%或%
二、数据类型
1. 数字
- rand:生成均匀分布的伪随机数,分布在(0~1)之间
- rand(m, n):生成m行n列的均匀分布的伪随机数
- rand(m, n, ‘double’):生成指定精度的均匀分布的伪随机数,参数还可以是’single’
- rand(RandStream, m, n)利用指定的RandStream(随机种子)生成为随机数
- randn:生成标准正态分布的伪随机数(均值为0,方差为1,语法同上)
- randi:生成均匀分布的伪随机数
- randi(iMax):在开区间(0,iMax)生成均匀分布的为随机整数
- randi(iMax):在开区间(0, iMax)生成m*n型随机矩阵
- randi([iMin, iMax], m, n):在开区间(iMin, iMax)生成m*n型随机矩阵
2. 字符与字符串
3. 矩阵
1 | A = [1 2 3; 4 5 6; 7 8 9] % 定义矩阵 |
4. 元胞数组ceil
- 元胞数组是MATLAB中特有的一种数据类型,是数组的一种,其内部元素可以是属于不同的数据类型,概念理解上,可以认为它和c语言里面的结构体、C++里面的对象很类似。元胞数组是matlab中的特色数据类型,它不同于其它数据类型(如字符型,字符数组或者叫字符串,以及一般的算术数据和数组)。它特有的存取数据方法决定了它的特点,它有给人一种查询信息的感觉,可以逐渐追踪一直到所有的变量全部翻译成基本的数据信息。它的class函数输出就是cell(细胞之意)。
1 | A = ceil(1, 6) % 生成一个1行5列的元胞数组 |
5. 结构体struct
1 | books = struct('name', {{'Math', 'English'}}, 'price', [30, 40]) |
三、矩阵操作
1. 矩阵定义与构造
1 | A = [1 2 3; 4 5 6; 7 8 9] |
2. 矩阵的四则运算
1 | C = A + B |
3. 矩阵下标
1 | B = A(2, 3) |
四、程序结构
1. for循环
1 | for 循环变量 = 初值:步长:中值 % 步长默认值为1 |
2. while循环
1 | while 条件表达式 |
3. if分支结构
1 | if 条件表达式 |
五、基本绘图操作
1. 二维平面绘图
1 | x = 0:0.01:2*pi; |
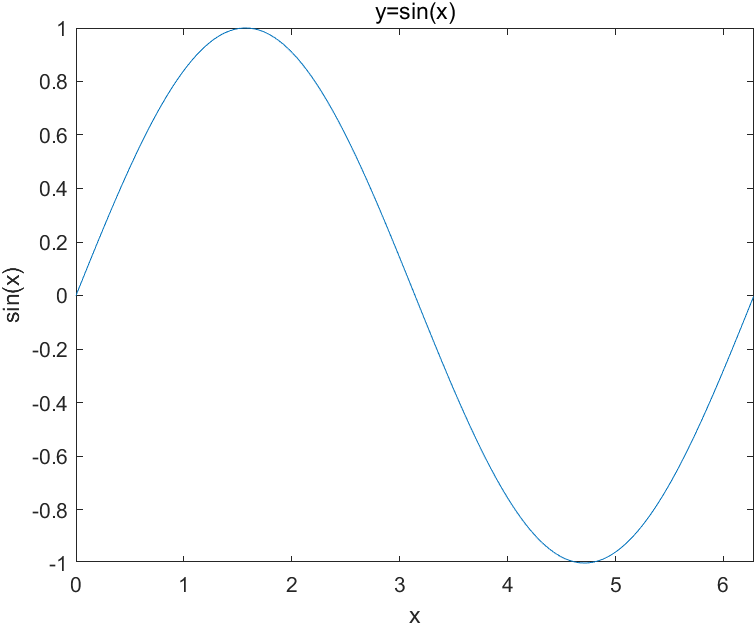
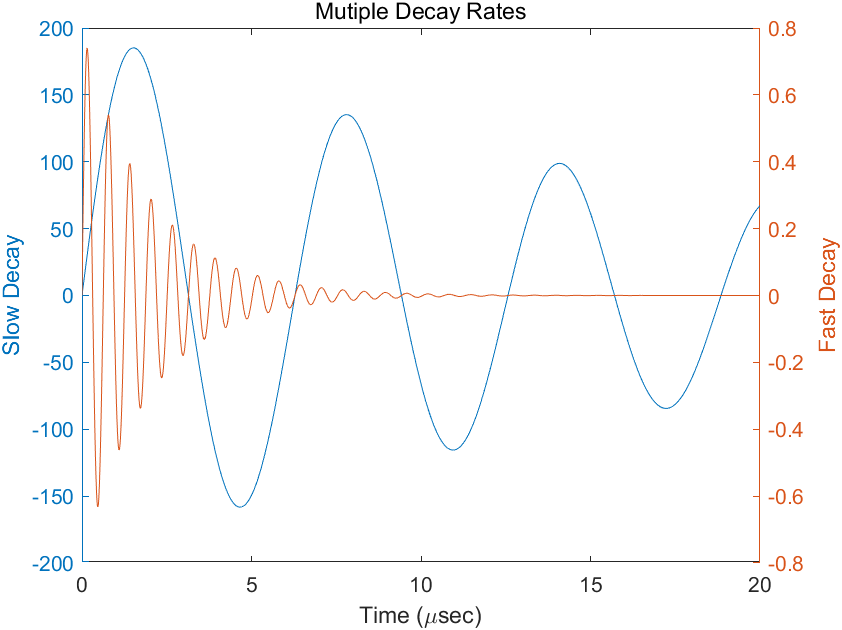
2. 绘制双Y曲线
1 | % 绘制双y曲线 |
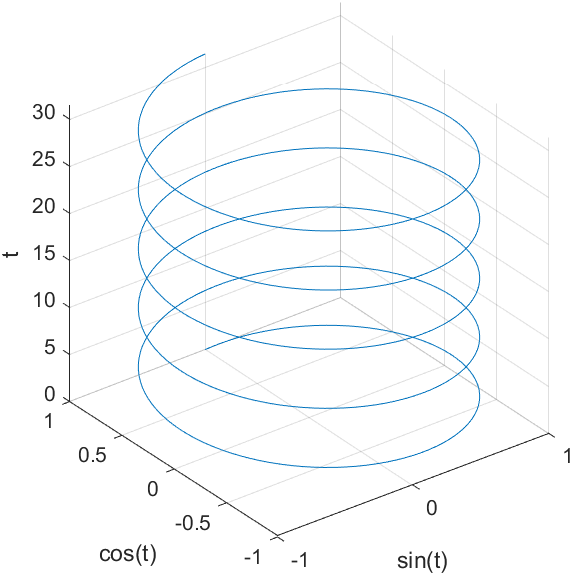
3. 三维绘图
1 | t = 0:pi/50:10*pi; |
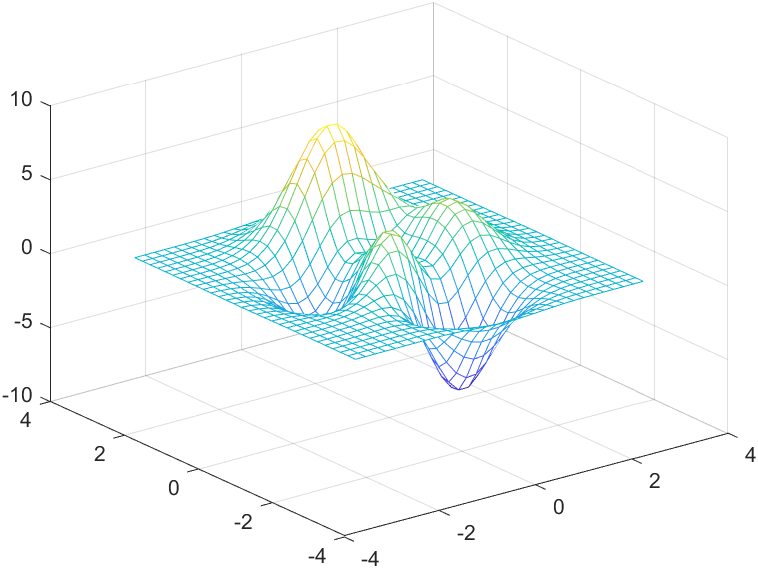
4. 双峰函数
1 | [x,y,z] = peaks(30); |
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Welcome to Durango's blog!!
评论

